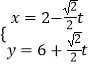Question

【题目】已知在Rt△AOB中，AO=1，BO=2，如图，动点P是在以O点为圆心，OB为半径的扇形内运动（含边界）且∠BOC=90°；设 ，则x+y的取值范围 ．

Answer 1

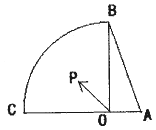
【答案】[﹣2,1]
【解析】解：以OA所在直线为x轴，以OB所在直线为y轴建立平面直角坐标系，如图所示；

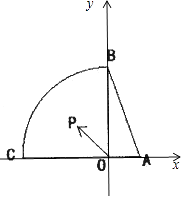
则A（1，0），B（0，2），

∴ =x +y =（x，0）+（0，2y）=（x，2y），

则x，y满足条件 ，

作出可行域如图所示，

令z=x+y，化目标函数为y=﹣x+z，

由图可知，当直线y=﹣x+z过点（0，1）时，直线在y轴上的截距最大，z有最大值1；

当直线y=﹣x+z过点（﹣2，0）时，直线在y轴上的截距最小，z有最小值﹣2；

则x+y的取值范围是[﹣2，1]．

所以答案是：[﹣2，1]．