题目内容
16.设f(n)=(a+b)n(n∈N*,n≥2),若f(n)的展开式中,存在某连续三项,其二项式系数依次差数列,则称f(n)具有性质P.(1)求证:f(7)具有性质P;
(2)若存在n≤2015,使用f(n)具有性质P,求n的最大值.
分析 (1)f(7)=(a+b)7,二、三、四项的二项式系数为7,21,35,依次成等差数列,可得结论;
(2)由题意,2Cnr=Cnr-1+Cnr+1,整理可得4r(n-r)=(n-2)(n+1),可得(n-2)(n+1)能被4整除,从而n-2或n+1为偶数时,必须能被4整除,结合n≤2015,即可求n的最大值.
解答 (1)证明:f(7)=(a+b)7,二、三、四项的二项式系数为7,21,35,依次成等差数列,
所以f(7)具有性质P.
(2)解:由题意,2Cnr=Cnr-1+Cnr+1,
整理可得4r(n-r)=(n-2)(n+1),
∴(n-2)(n+1)能被4整除,
∵n-2、n+1一奇一偶,
∴n-2或n+1为偶数时,必须能被4整除,
∵n≤2015
∴n的最大值为2012.
点评 本题考查二项式定理的运用,考查学生对定义的理解,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.某几何体三视图如下,图中三个等腰三角形的直角边长都是2,该几何体的体积为( )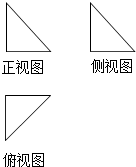

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
7.执行如图所示的程序框图,则输出的i的值是( )
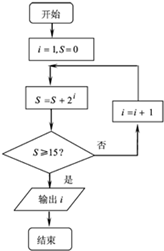

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
11.过球面上任意两点,可以作大圆的个数为( )
| A. | 1个 | B. | 2个 | C. | 无数多个 | D. | 1个或无数多个 |
5.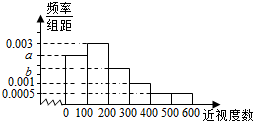 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
将近视程度由低到高分为4个等级:当近视度数在0-100时,称为不近视,记作0;当近视度数在100-200时,称为轻度近视,记作1;当近视度数在200-400时,称为中度近视,记作2;当近视度数在400以上时,称为高度近视,记作3.
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
(Ⅰ)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(Ⅱ)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(Ⅲ)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.