题目内容
已知集合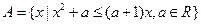 .
.
(1)是否存在实数 ,使得集合
,使得集合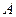 中所有整数
中所有整数 的元素和为28?若存在,求出符合条件的
的元素和为28?若存在,求出符合条件的 ,若不存在,请说明理由。
,若不存在,请说明理由。
(2)若以 为首项,
为首项, 为公比的等比数列前
为公比的等比数列前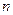 项和记为
项和记为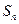 ,对于任意的
,对于任意的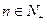 ,均有
,均有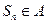 ,求
,求 的取值范围。
的取值范围。
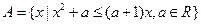 .
.(1)是否存在实数
 ,使得集合
,使得集合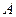 中所有整数
中所有整数 的元素和为28?若存在,求出符合条件的
的元素和为28?若存在,求出符合条件的 ,若不存在,请说明理由。
,若不存在,请说明理由。(2)若以
 为首项,
为首项, 为公比的等比数列前
为公比的等比数列前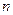 项和记为
项和记为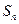 ,对于任意的
,对于任意的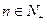 ,均有
,均有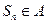 ,求
,求 的取值范围。
的取值范围。(1)当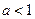 时,不符合;当
时,不符合;当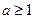 时,存在,
时,存在,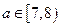 (2)
(2) 的取值范围是
的取值范围是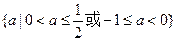
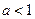 时,不符合;当
时,不符合;当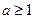 时,存在,
时,存在,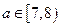 (2)
(2) 的取值范围是
的取值范围是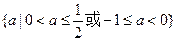
(1) 当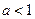 时,
时,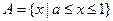 ,不符合;
,不符合;
当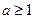 时,
时,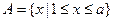 ,设
,设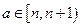 ,
,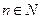 ,则1+2+…+n=
,则1+2+…+n=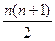 =28,所以n=7,即
=28,所以n=7,即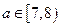
(2)?当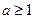 时,
时,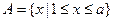 .而
.而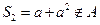 ,故
,故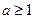 时,不存在满足条件的
时,不存在满足条件的 ;
;
?当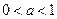 时,
时,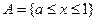 ,而
,而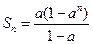 是关于
是关于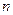 的增函数,所以
的增函数,所以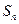 随
随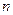 的增大而增大,当
的增大而增大,当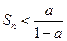 且无限接近
且无限接近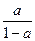 时,对任意的
时,对任意的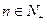 ,
,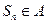 ,只须
,只须 满足
满足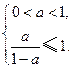 解得
解得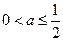 .
.
?当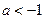 时,
时,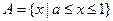 .
.
而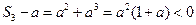 ,
,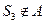 故不存在实数
故不存在实数 满足条件.
满足条件.
④ 当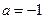 时,
时,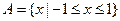 .
.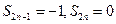 ,适合.
,适合.
⑤当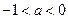 时,
时,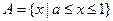 .
.
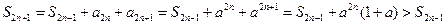 ,
,
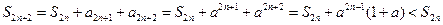 ,
,
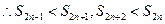 ,且
,且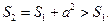
故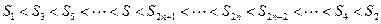 .
.
故只需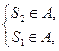 即
即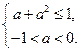 解得
解得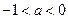 .
.
综上所述, 的取值范围是
的取值范围是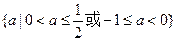
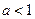 时,
时,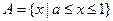 ,不符合;
,不符合;当
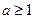 时,
时,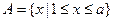 ,设
,设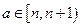 ,
,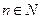 ,则1+2+…+n=
,则1+2+…+n=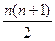 =28,所以n=7,即
=28,所以n=7,即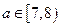
(2)?当
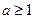 时,
时,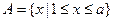 .而
.而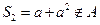 ,故
,故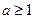 时,不存在满足条件的
时,不存在满足条件的 ;
;?当
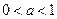 时,
时,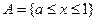 ,而
,而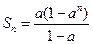 是关于
是关于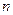 的增函数,所以
的增函数,所以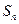 随
随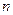 的增大而增大,当
的增大而增大,当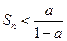 且无限接近
且无限接近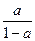 时,对任意的
时,对任意的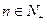 ,
,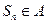 ,只须
,只须 满足
满足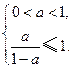 解得
解得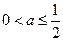 .
.?当
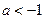 时,
时,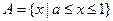 .
.而
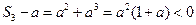 ,
,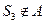 故不存在实数
故不存在实数 满足条件.
满足条件.④ 当
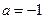 时,
时,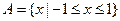 .
.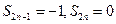 ,适合.
,适合.⑤当
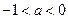 时,
时,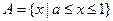 .
.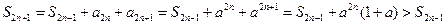 ,
,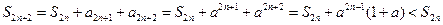 ,
,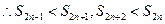 ,且
,且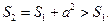
故
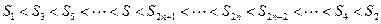 .
.故只需
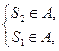 即
即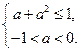 解得
解得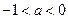 .
.综上所述,
 的取值范围是
的取值范围是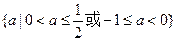

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
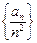
 是公比为
是公比为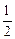 的等比数列,
的等比数列,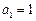 .
.
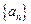 的通项公式;
的通项公式;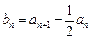 ,若数列
,若数列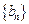 的前
的前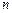 项和
项和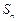 ,求证:
,求证:
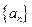 的公比
的公比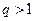 ,
,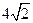 是
是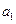 和
和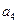 的一个等比中项,
的一个等比中项,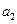 和
和 的等差中项为
的等差中项为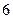 ,若数列
,若数列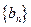 满足
满足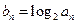 (
( ).
).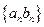 的前
的前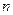 项和
项和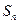 .
. a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)
a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)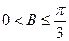 ;(2)
;(2)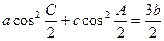 ;(3)
;(3)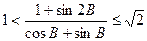 。
。 _______
_______ __________________
__________________ (II)证明:
(II)证明: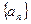 ,如果存在非零实数
,如果存在非零实数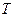 使得
使得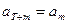 对于任意的正整数
对于任意的正整数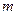 均成立,那么称
均成立,那么称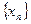 满足
满足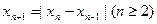 ,如果
,如果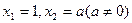 ,当数列
,当数列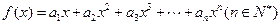 ,满足
,满足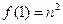 ,
,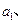
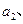
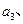
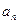 构成数列
构成数列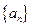 。
。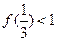 。
。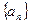 满足
满足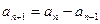
 ,
,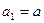 ,
,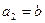 ,
,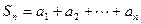 ,则下列结论正确的是
,则下列结论正确的是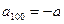 ,
,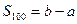
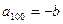 ,
,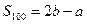
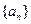 中,
中,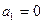 ,
, ,则
,则 ( )
( )


