题目内容
△ABC的三个内角A、B、C的对边的长分别为 a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)
a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)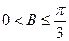 ;(2)
;(2)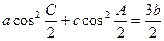 ;(3)
;(3)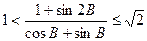 。
。
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之。
(I)组建的命题为:已知_______________________________________________
求证:①_________________ _______
_______ __________________
__________________
②__________________________________________
 (II)证明:
(II)证明:
 a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)
a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)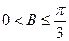 ;(2)
;(2)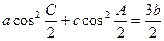 ;(3)
;(3)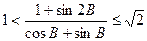 。
。请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之。
(I)组建的命题为:已知_______________________________________________
求证:①_________________
 _______
_______ __________________
__________________②__________________________________________
 (II)证明:
(II)证明: 略
可以组建命题一:△ABC中,若a、b、c成等差数列,求证:(1)0<B≤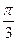
(2)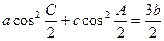 ;
;
命题二:△ABC中,若a、b、c成等差数列求证:(1)0<B≤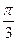
(2)1<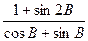 ≤
≤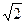
命题三:△ABC中,若a、b、c成等差数列,求证:(1)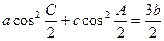
 (2)1<
(2)1<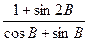 ≤
≤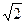
命题四:△ABC中,若a、b、c成等比数列,求证:(1)0<B≤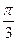
(2)1<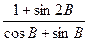 ≤
≤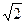
下面给出命题一、二、三的证明:
(1)∵a、b、c成等差数列∴2b=a+c,∴b=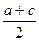
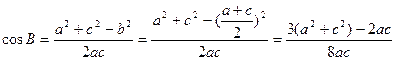 ≥
≥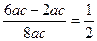

且B∈(0,π),∴0<B≤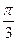
(2)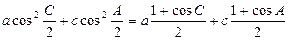
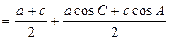
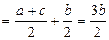
(3)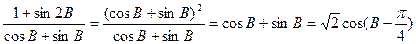
∵0<B≤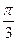 ∴
∴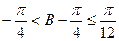 ∴
∴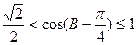
∴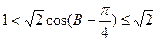
下面给出命题四的证明:
(4)∵a、b、c成等比数列∴b2=a+c,
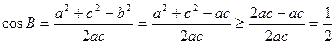
且B ∈(
∈( 0,π),∴0<B≤
0,π),∴0<B≤
(2)
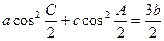 ;
;命题二:△ABC中,若a、b、c成等差数列求证:(1)0<B≤
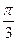
(2)1<
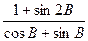 ≤
≤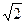
命题三:△ABC中,若a、b、c成等差数列,求证:(1)
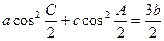
 (2)1<
(2)1<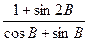 ≤
≤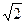
命题四:△ABC中,若a、b、c成等比数列,求证:(1)0<B≤
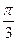
(2)1<
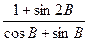 ≤
≤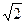
下面给出命题一、二、三的证明:
(1)∵a、b、c成等差数列∴2b=a+c,∴b=
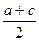
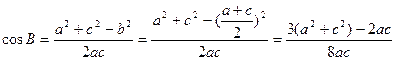 ≥
≥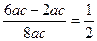

且B∈(0,π),∴0<B≤
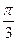
(2)
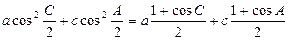
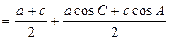
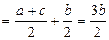
(3)
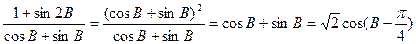
∵0<B≤
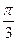 ∴
∴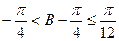 ∴
∴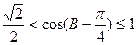
∴
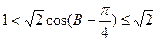
下面给出命题四的证明:
(4)∵a、b、c成等比数列∴b2=a+c,
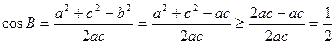
且B
 ∈(
∈( 0,π),∴0<B≤
0,π),∴0<B≤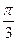

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
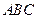 中,
中,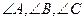 所对的边分别为
所对的边分别为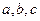 ,满足
,满足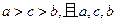 成等差数列,
成等差数列,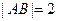 ,求点
,求点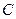 的轨迹方程.
的轨迹方程. .
.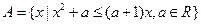 .
. ,使得集合
,使得集合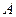 中所有整数
中所有整数 的元素和为28?若存在,求出符合条件的
的元素和为28?若存在,求出符合条件的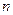 项和记为
项和记为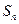 ,对于任意的
,对于任意的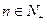 ,均有
,均有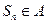 ,求
,求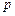 ,
,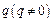 是实数,方程
是实数,方程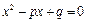 有两个实根
有两个实根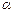 ,
,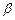 ,数列
,数列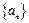 满足
满足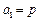 ,
,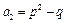 ,
,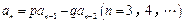
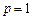 ,
,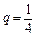 ,求
,求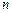 项和.
项和.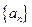 的前n项和为
的前n项和为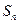 ,若对任意的r、s
,若对任意的r、s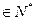 ,都有
,都有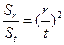 .
.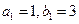 ,数列
,数列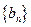 的第n项是数列
的第n项是数列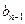 项
项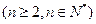 ,求
,求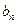 ;
;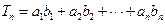 .
.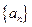 的前
的前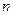 项和为
项和为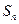
 且满足:
且满足: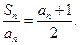
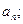
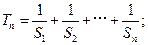
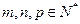 且
且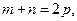 求证:
求证: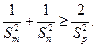
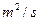 的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2
的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2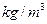 和0.2
和0.2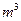 的水量,即从A股流入B股100
的水量,即从A股流入B股100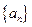 和
和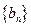 的前
的前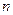 项和分别为
项和分别为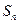 和
和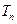 ,且
,且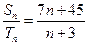 ,则使得
,则使得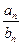 为整数的正整数
为整数的正整数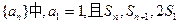 成等差数列
成等差数列 ,则
,则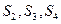 分别为 ,由此猜想出
分别为 ,由此猜想出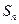 = 。
= 。