题目内容
19.己知f(x)=x3-ax在[1,+∞)上是单调增函数,则a的取值范围是( )| A. | (3,+∞) | B. | (1,3) | C. | (-∞,3) | D. | (-∞,3] |
分析 由f(x)=x3-ax在[1,+∞)上是单调增函数,得f′(x)=3x2-a≥0在[1,+∞)上恒成立,分离参数a后求出函数y=3x2在[1,+∞)上的最小值得答案.
解答 解:∵f(x)=x3-ax在[1,+∞)上是单调增函数,
∴f′(x)=3x2-a≥0在[1,+∞)上恒成立.
即a≤3x2在[1,+∞)上恒成立.
∵y=3x2在[1,+∞)上为增函数,∴ymin=3.
∴a≤3.
故选:D.
点评 本题考查函数的单调性与导函数符号间的关系,考查分离参数方法,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.若某几何体的三视图如图所示,则此几何体的体积是( )
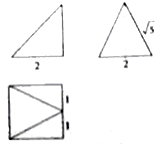

| A. | 4$\sqrt{5}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
 对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为100.
对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为100.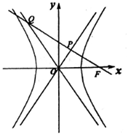 如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2.
如图,F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点,过F作渐近线的垂线,垂足为P,与另一条渐近线相交于Q,若|PF|=|PQ|,则C的离心率为2. 图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2
图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2 (Ⅰ)求抛物线C的方程;
(Ⅰ)求抛物线C的方程;