题目内容
2.设l,m,n表示三条不同的直线,α,β,γ表示三个不同的平面,给出下列四个命题:①若l⊥α,m⊥l,m⊥β,则α⊥β;
②若m?β,n是l在m⊥l内的射影,m⊥l,则m⊥l;
③若m是平面α的一条斜线,A∉α,l为过A的一条动直线,则可能有l⊥m且l⊥α;
④若α⊥β,α⊥γ,则γ∥β
其中真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用空间线面关系定理分别对四个命题分析选择.①由空间向量知识可知正确;②由三垂线定理可证;③④可举反例说明错误
解答 解:对于①若l⊥α,m⊥l,m⊥β,由空间线面垂直的性质定理可知α⊥β正确;
②若m?β,n是l在m⊥l内的射影,m⊥l,则m⊥l;由三垂线定理知正确;
③若m是平面α的一条斜线,A∉α,l为过A的一条动直线,则可能有l⊥m且l⊥α;
若m是平面α的一条斜线,l⊥α,则l和m不可能垂直,故命题错误;
④若α⊥β,α⊥γ,则γ∥β错误;如墙角的三个面的关系;
故选:B.
点评 本题考查空间的线面位置关系,考查空间想象能力和逻辑推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.当直线y=kx与曲线y=|x|-|x-2|有3个公共点时,实数k的取值范围是( )
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
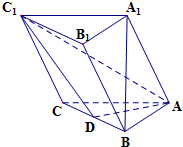 如图,在三棱柱ABC-A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=$\sqrt{2}$.求证:
如图,在三棱柱ABC-A1B1C1中,D为棱BC的中点,AB⊥BC,BC⊥BB1,AB=A1B=1,BB1=$\sqrt{2}$.求证: