题目内容
11.已知tan2α=$\frac{3}{4}$,α∈$({-\frac{π}{2},\frac{π}{2}})$,f(x)=sin(x+α)+sin(α-x)-2sinα,且对任意的x∈R,恒有f(x)≥0成立,试求$sin(α-\frac{π}{4})$的值.分析 首先对所给的三角函数式进行整理,得到最简形式,根据有对任意x∈R,都有f(x)≥0成立这种恒成立问题,分析两个因式的符号,根据符号确定角的范围,根据同角的三角函数关系和两角差的正弦公式计算得到结果.
解答 解:依题意f(x)=2sinαcosx-2sinα=2sinα(cosx-1)
由对任意x∈R,都有f(x)≥0成立,
∵cosx-1≤0,
∴sinα≤0,
∴-$\frac{π}{2}$≤α≤0,
由tan2α=$\frac{3}{4}$,即$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{3}{4}$,
得tanα=-3,($\frac{1}{3}$舍去),
∴sinα=-$\frac{3}{\sqrt{10}}$,cosα=$\frac{\sqrt{10}}{10}$,
则$sin(α-\frac{π}{4})$=$\frac{\sqrt{2}}{2}$(sinα-cosα)=$\frac{\sqrt{2}}{2}$×(-$\frac{2\sqrt{10}}{5}$)=-$\frac{2\sqrt{5}}{5}$.
点评 本题主要考查函数恒成立问题,本题解题的关键是利用函数的恒成立确定两个因式的符号,从而确定角的范围,本题是一个比较综合的题目.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
4.半径为1的球的表面积为( )
| A. | 1 | B. | 2π | C. | 3π | D. | 4π |
3.f(x)是定义在[-3,3]上的奇函数,且x>0时,f′(x)cosx<f(x)sinx则不等式f(x)cosx>0的解集是( )
| A. | [-3,0] | B. | $(-\frac{π}{2},0)∪(\frac{π}{2},3]$ | C. | $[-3,-\frac{π}{2})∪(\frac{π}{2},3]$ | D. | $[-3,-\frac{π}{2})∪(0,\frac{π}{2})$ |
1.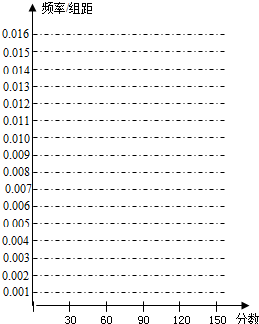 我校高二期中考试统一测试文科的数学成绩分组统计如下表:
我校高二期中考试统一测试文科的数学成绩分组统计如下表:
(Ⅰ)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
(Ⅱ)若我校参加本次考试的文科学生有600人,试估计这次测试中我校成绩在90分以上的人数;
(Ⅲ)若我校教师拟从分数不超过60分的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
 我校高二期中考试统一测试文科的数学成绩分组统计如下表:
我校高二期中考试统一测试文科的数学成绩分组统计如下表:(Ⅰ)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
| 分组 | 频数 | 频率 |
| (0,30] | 3 | 0.03 |
| (30,60] | 3 | 0.03 |
| (60,90] | 37 | 0.37 |
| (90,120] | m | n |
| (120,150] | 15 | 0.15 |
| 合计 | M | N |
(Ⅲ)若我校教师拟从分数不超过60分的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
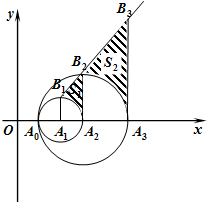 如图,在平面直角坐标系xOy中,设a1=2,有一组圆心在x轴正半轴上的圆An(n=1,2,…)与x轴的交点分别为A0(1,0)和An+1(an+1,0).过圆心An作垂直于x轴的直线ln,在第一象限与圆An交于点Bn(an,bn).
如图,在平面直角坐标系xOy中,设a1=2,有一组圆心在x轴正半轴上的圆An(n=1,2,…)与x轴的交点分别为A0(1,0)和An+1(an+1,0).过圆心An作垂直于x轴的直线ln,在第一象限与圆An交于点Bn(an,bn).