题目内容
(2011•湖北)已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax﹣a﹣x+2(a>0,且a≠0).若g(a)=a,则f(a)=( )
| A.2 | B.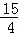 | C.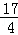 | D.a2 |
B
∵f(x)是定义在R上的奇函数,g(x)是定义在R上的偶函数
由f(x)+g(x)=ax﹣a﹣x+2 ①
得f(﹣x)+g(﹣x)=a﹣x﹣ax+2=﹣f(x)+g(x) ②
①②联立解得f(x)=ax﹣a﹣x,g(x)=2
由已知g(a)=a
∴a=2
∴f(a)=f(2)=22﹣2﹣2=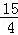
故选B
由f(x)+g(x)=ax﹣a﹣x+2 ①
得f(﹣x)+g(﹣x)=a﹣x﹣ax+2=﹣f(x)+g(x) ②
①②联立解得f(x)=ax﹣a﹣x,g(x)=2
由已知g(a)=a
∴a=2
∴f(a)=f(2)=22﹣2﹣2=
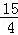
故选B

练习册系列答案
相关题目
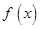 的定义域为D,如果
的定义域为D,如果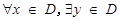 ,使得
,使得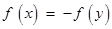
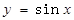 ;
;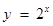 ;③
;③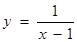 ;④
;④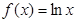 , 则其中“Ω函数”共有( )
, 则其中“Ω函数”共有( )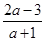 ,则实数a的取值范围是________.
,则实数a的取值范围是________.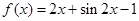 图像的对称中心是 .
图像的对称中心是 .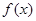 是定义在
是定义在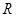 上的偶函数,当
上的偶函数,当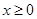 时,
时,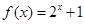 ,若
,若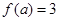 ,则实数
,则实数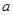 的值为 .
的值为 .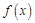 是定义在
是定义在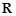 上的奇函数,当
上的奇函数,当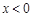 时,
时,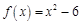 ,则
,则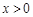 时,
时,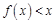 的解集为________.
的解集为________. 上的函数
上的函数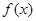 是奇函数且满足
是奇函数且满足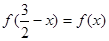 ,
,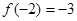 ,数列
,数列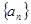 满足
满足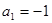 ,且
,且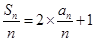 ,(其中
,(其中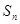 为
为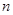 项和),则
项和),则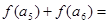 ( ).
( ).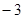
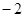
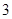
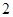
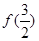 =
=