题目内容
【题目】已知抛物线![]() ,直线
,直线![]() (
(![]() )与
)与![]() 交于
交于![]() 两点,
两点,![]() 为
为![]() 的中点,
的中点,![]() 为坐标原点.
为坐标原点.
(1)求直线![]() 斜率的最大值;
斜率的最大值;
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() 为等边三角形,求点
为等边三角形,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
解法一:(1)设![]() 两点坐标,将直线方程与抛物线方程联立,根据一元二次方程根与系数关系、根的判别式、中点坐标公式求出
两点坐标,将直线方程与抛物线方程联立,根据一元二次方程根与系数关系、根的判别式、中点坐标公式求出![]() 的坐标,最后根据斜率公式,结合基本不等式进行求解即可;
的坐标,最后根据斜率公式,结合基本不等式进行求解即可;
(2)利用弦长公式求出等边三角形的边长,最后利用等边三角形的性质,得到方程,求解方程即可求出点![]() 的坐标.
的坐标.
解法二:(1)设出![]() 两点的坐标,根据点在抛物线上,得到两个方程,再利用
两点的坐标,根据点在抛物线上,得到两个方程,再利用![]() 两点在直线上、中点坐标公式求出
两点在直线上、中点坐标公式求出![]() 的坐标,最后根据斜率公式,结合基本不等式进行求解即可;
的坐标,最后根据斜率公式,结合基本不等式进行求解即可;
(2)将直线方程与抛物线方程联立,根据一元二次方程根与系数关系、根的判别式、两点间距离公式求出等边三角形的边长,最后利用等边三角形的性质,得到方程,求解方程即可求出点![]() 的坐标.
的坐标.
解法一:(1)设![]() ,
,
由![]() ,消去
,消去![]() 得,
得,![]() ,
,
![]() 且
且![]() .
.
所以![]()
因为![]() 为
为![]() 的中点,
的中点,
所以![]() 的坐标为
的坐标为![]() ,即
,即![]() ,
,
又因为![]() ,所以
,所以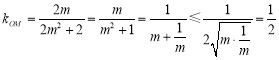 ,
,
(当且仅当![]() ,即
,即![]() 等号成立.)
等号成立.)
所以![]() 的斜率的最大值为
的斜率的最大值为![]() ;
;
(2)由(1)知,
![]()
![]()
![]()
![]() ,
,
由![]() 得
得![]() ,
,
因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,解得
,解得![]()
又![]() ,所以
,所以![]() ,
,
则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
所以![]() 时,
时,![]() ,
,
所以所求的点![]() 的坐标为
的坐标为![]() .
.
解法二:(1)设![]() ,
,
因为![]() 为
为![]() 的中点,且直线
的中点,且直线![]() ,
,
所以![]() 因为
因为![]() ,
,![]() ,两个等式相减得:
,两个等式相减得:![]()
由 得
得![]()
所以![]() 所以
所以![]() 即
即![]() .
.
所以![]() 即
即![]() ,
,
又因为![]() ,所以
,所以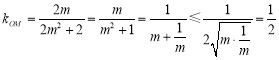 ,
,
(当且仅当![]() ,即
,即![]() 等号成立.)
等号成立.)
所以![]() 的斜率的最大值为
的斜率的最大值为![]() .
.
(2)由![]() ,消去
,消去![]() 得
得![]() ,
,
所以![]() 且
且![]() .
.
![]()
![]()
![]()
![]()
![]() ,
,
由(1)知,![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
所以线段![]() 的垂直平分线方程为:
的垂直平分线方程为:![]() .
.
令![]() ,得线段
,得线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 交点坐标为
交点坐标为![]()
所以![]() .
.
因为![]() 为等边三角形,所以
为等边三角形,所以![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,解得
,解得![]()
因为![]() 所以
所以![]() ,
,
则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
所以![]() 时,
时,![]() ,
,
所以所求的点![]() 的坐标为
的坐标为![]() .
.

【题目】2020年新年伊始,新型冠状病毒来势汹汹,疫情使得各地学生在寒假结束之后无法返校,教育部就此提出了线上教学和远程教学,停课不停学的要求也得到了家长们的赞同.各地学校开展各式各样的线上教学,某地学校为了加强学生爱国教育,拟开设国学课,为了了解学生喜欢国学是否与性别有关,该学校对100名学生进行了问卷调查,得到如下列联表:
喜欢国学 | 不喜欢国学 | 合计 | |
男生 | 20 | 50 | |
女生 | 10 | ||
合计 | 100 |
(1)请将上述列联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系?
(2)针对问卷调查的100名学生,学校决定从喜欢国学的人中按分层抽样的方法随机抽取6人成立国学宣传组,并在这6人中任选2人作为宣传组的组长,求选出的两人均为女生的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
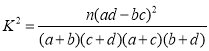 ,
,![]() .
.