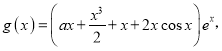题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 经过椭圆C的左、右焦点
经过椭圆C的左、右焦点![]() ,
,![]() .
.
(1)求椭圆C的标准方程;
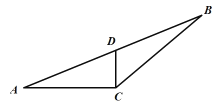
(2)若A,B,D,E是椭圆C上不同四点(其中点D在第一象限),且![]() ,直线
,直线![]() ,
,![]() 关于直线
关于直线![]() 对称,求直线
对称,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据离心率可得![]() ,根据圆
,根据圆![]() 经过椭圆C的左、右焦点
经过椭圆C的左、右焦点![]() ,
,![]() 可得
可得![]() ,进而可得方程;
,进而可得方程;
(2)根据对称性可得![]() ,设出
,设出![]() 的方程,结合韦达定理和对称性求出
的方程,结合韦达定理和对称性求出![]() 的坐标,进而得到
的坐标,进而得到![]() 的斜率,结合直线平行可求直线
的斜率,结合直线平行可求直线![]() 的方程.
的方程.
(1)设![]() ,由题意得
,由题意得![]() ,
,
由圆![]() 经过椭圆C的左,右焦点
经过椭圆C的左,右焦点![]() ,
,![]() 得
得![]() ,
,
所以![]() ,
,![]() ,
,
所以椭圆C的标准方程为![]() .
.
(2)由题意可得![]() ,且直线
,且直线![]() 的斜率存在,设
的斜率存在,设![]() ,
,![]() ,
,![]() .
.
把![]() 与椭圆方程
与椭圆方程![]() 联立,
联立,
得![]() .
.
所以![]() ,
,
所以![]() ,
,![]() ,
,
由直线![]() ,
,![]() 关于直线
关于直线![]() 对称,可得直线
对称,可得直线![]() 的斜率为
的斜率为![]() .
.
用![]() 代替k,得
代替k,得![]() ,
,![]() ,
,
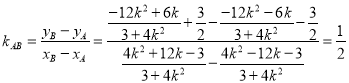 .
.
又![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.

【题目】某疾病有甲、乙两种类型,对甲型患者的有效治疗只能通过注射药物Y,而乙型患者可以服药物A进行有效治疗,对该疾病患者可以通过药物A的临床检验确定甲型或乙型.检验的方法是:如果患者利用药物A完成第一个疗程有效,就可以确定是乙型;否则进行第二个疗程,如果完成第二个疗程有效,也可以确定是乙型,否则确定是甲型.为了掌握这种疾病患者中甲型、乙型所占比例,随机抽取100名患者作为样本通过药物A进行临床检验,检验结果是:样本中完成第二个疗程有效的患者是完成第一个疗程有效的患者的60%,且最终确定为甲型患者的有36人.
(1)根据检验结果,将频率视作概率,在利用药物A完成第一个疗程无效的患者中仼选3人,求其中甲型患者恰为2人的概率;
(2)该疾病的患者通过治疗,使血浆中某物质t的浓度降低到![]() 或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:
或更低时,就认为已经达到治愈指标.为了确定药物Y对甲型患者的疗效,需了解疗程次数x(单位:次)对患者血浆中t的浓度(单位:![]() )的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数
)的影响.在甲型患者中抽取一个有代表性的样本,利用药物Y进行5个疗程,每个疗程完成后对每个个体抽取相同容量的血浆进行分析,并对疗程数![]() 和每个疗程后样本血浆中t的平均浓度
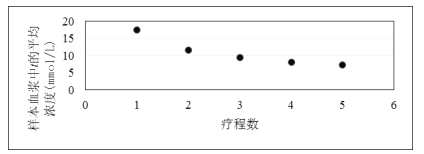
和每个疗程后样本血浆中t的平均浓度![]() 的数据作了初步处理,得到下面的散点图及一些统计量的值.
的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
3 | 11.0 | 0.46 | 262.5 | 30.1 | 55 | 1.458 |
/span>
上表中![]() ,
,![]() .
.
①根据散点图直接判断(不必说明理由),![]() 与
与![]() 哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
哪一个适宜作为甲型患者血浆中t的平均浓度y关于疗程次数x的回归方程类型?并根据表中数据建立y关于x的回归方程.
②患者在享受基本医疗保险及政府专项补助后,自己需承担的费用z(单位:元)与x,y的关系为![]() .在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
.在达到治愈指标的前提下,甲型患者完成多少个疗程自己承担的费用最低?
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为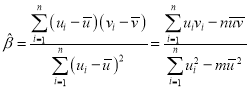 ,
,![]() .
.