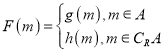题目内容
【题目】已知函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)是否存在实数![]() ,使得
,使得![]() 有三个相异零点?若存在,求出
有三个相异零点?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(Ⅰ)见解析.(Ⅱ)见解析.
【解析】试题分析:(I)求出![]() ,分三种情况讨论
,分三种情况讨论![]() 的范围,分别令
的范围,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(II)假设
的减区间;(II)假设![]() 有三个相异零点,由(Ⅰ)的讨论可知,一定有
有三个相异零点,由(Ⅰ)的讨论可知,一定有![]() 且
且![]() 的极大值大于0,极小值小于0,则取得极大值和极小值时
的极大值大于0,极小值小于0,则取得极大值和极小值时![]() 或
或![]() ,注意到此时恒有
,注意到此时恒有![]() ,则必有
,则必有![]() 为极小值,此时极值点满足
为极小值,此时极值点满足![]() ,即
,即![]() ,还需满足
,还需满足![]() ,换元后只需证明
,换元后只需证明![]() 即可.
即可.
试题解析:(Ⅰ)由题可知![]()
![]()
![]() .
.
当![]() ,即
,即![]() 时,令
时,令![]() 得
得![]() ,易知
,易知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() 时,令
时,令![]() 得
得![]() 或
或![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)不存在.
理由如下:假设![]() 有三个相异零点.
有三个相异零点.
由(Ⅰ)的讨论,一定有![]() 且
且![]() 的极大值大于0,极小值小于0.
的极大值大于0,极小值小于0.
已知取得极大值和极小值时![]() 或
或![]() ,
,
注意到此时恒有![]() ,则必有
,则必有![]() 为极小值,
为极小值,
此时极值点满足![]() ,即
,即![]() ,还需满足
,还需满足![]() ,
,
又![]()
![]() ,
,![]() ,
,
故存在![]() 使得
使得![]() ,即存在
,即存在![]() 使得
使得![]() .
.
令![]() ,即存在
,即存在![]() 满足
满足![]() .
.
令![]() ,
,![]() ,从而
,从而![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
故不存在![]() 满足
满足![]() ,与假设矛盾,从而不存在
,与假设矛盾,从而不存在![]() 使得
使得![]() 有三个相异零点.
有三个相异零点.

【题目】从2017年1月18日开始,支付宝用户可以通过“![]() 扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福、敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
扫‘福’字”和“参与蚂蚁森林”两种方式获得福卡(爱国福、富强福、和谐福、友善福、敬业福),除夕夜22:18,每一位提前集齐五福的用户都将获得一份现金红包.某高校一个社团在年后开学后随机调查了80位该校在读大学生,就除夕夜22:18之前是否集齐五福进行了一次调查(若未参与集五福的活动,则也等同于未集齐五福),得到具体数据如下表:
| 是 | 否 | 合计 |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)根据如上的列联表,能否在犯错误的概率不超过0.05的前提下,认为“集齐五福与性别有关”?
(2)计算这80位大学生集齐五福的频率,并据此估算该校10000名在读大学生中集齐五福的人数;
(3)为了解集齐五福的大学生明年是否愿意继续参加集五福活动,该大学的学生会从集齐五福的学生中,选取2位男生和3位女生逐个进行采访,最后再随机选取3次采访记录放到该大学的官方网站上,求最后被选取的3次采访对象中至少有一位男生的概率.
参考公式:![]()
![]()
![]() .
.
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |