题目内容
(本小题满分14分)
已知双曲线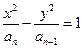 的一个焦点为(
的一个焦点为(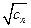 ,0),一条渐近线方程为
,0),一条渐近线方程为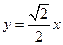 ,其中
,其中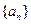
是以4为首项的正数数列,记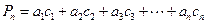 .
.
(Ⅰ)求数列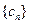 的通项公式;
的通项公式;
(Ⅱ)若数列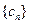 的前n项的和为Sn,求
的前n项的和为Sn,求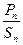 ;
;
(Ⅲ)若不等式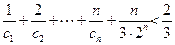 +
+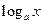 (a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
(a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
已知双曲线
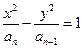 的一个焦点为(
的一个焦点为(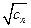 ,0),一条渐近线方程为
,0),一条渐近线方程为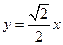 ,其中
,其中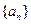
是以4为首项的正数数列,记
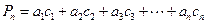 .
.(Ⅰ)求数列
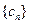 的通项公式;
的通项公式; (Ⅱ)若数列
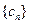 的前n项的和为Sn,求
的前n项的和为Sn,求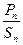 ;
;(Ⅲ)若不等式
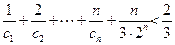 +
+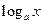 (a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
(a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.解: (Ⅰ)∵双曲线方程为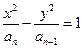 的一个焦点为(
的一个焦点为(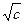 ,0),∴
,0),∴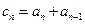 .
.
又∵一条渐近线方程为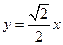 ,∴
,∴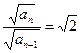 .∴
.∴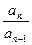 =2.
=2.
∵a1=4,∴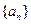 是以4为首项的等比数列,an=2n+1.∴cn=3·2n.
是以4为首项的等比数列,an=2n+1.∴cn=3·2n.
(Ⅱ) Sn=c1+c2+…+cn=3(2+22+…+2n)=6(2n-1).
∵ancn=3·22n+1,
∴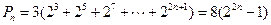
∴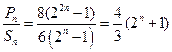
(Ⅲ)T=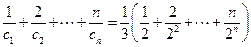 ,①
,①
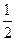 T=
T=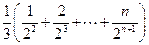 ,②
,②
①-②得T=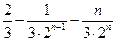 ,
,
故原不等式等价于
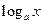 (n∈N*)恒成立,即
(n∈N*)恒成立,即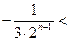
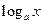 恒成立,
恒成立,
∴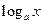 ≥0恒成立,
≥0恒成立,
故(ⅰ)当a>1时,x≥1.(ⅱ)当0<a<1时,0<x≤1.
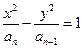 的一个焦点为(
的一个焦点为(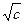 ,0),∴
,0),∴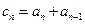 .
.又∵一条渐近线方程为
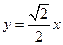 ,∴
,∴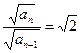 .∴
.∴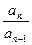 =2.
=2.∵a1=4,∴
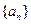 是以4为首项的等比数列,an=2n+1.∴cn=3·2n.
是以4为首项的等比数列,an=2n+1.∴cn=3·2n.(Ⅱ) Sn=c1+c2+…+cn=3(2+22+…+2n)=6(2n-1).
∵ancn=3·22n+1,
∴
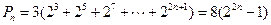
∴
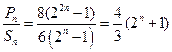
(Ⅲ)T=
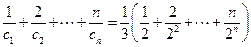 ,①
,①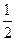 T=
T=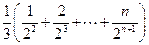 ,②
,②①-②得T=
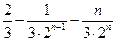 ,
,故原不等式等价于

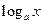 (n∈N*)恒成立,即
(n∈N*)恒成立,即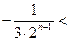
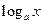 恒成立,
恒成立,∴
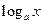 ≥0恒成立,
≥0恒成立,故(ⅰ)当a>1时,x≥1.(ⅱ)当0<a<1时,0<x≤1.
略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
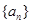 的首项为3,
的首项为3,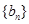 为等差数列且
为等差数列且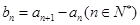 ,若
,若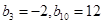 ,则
,则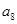 = ( )
= ( )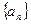 的通项公式为
的通项公式为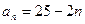 ,求数列
,求数列


 的各项均为正数,
的各项均为正数, 为其前n项和,对于任意的
为其前n项和,对于任意的 ,满足关系式
,满足关系式
 的通项公式;
的通项公式; 的通项公式是
的通项公式是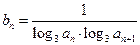 ,求
,求 .
.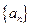 的前
的前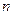 项和为
项和为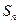 ,对任意的
,对任意的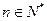 ,点
,点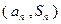 都在直线
都在直线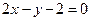 的图像上.
的图像上.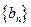 ,使得
,使得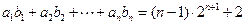 对一切
对一切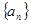 中,各项都是正数,且
中,各项都是正数,且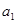 ,
,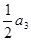 ,
,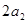 成等差数列,则
成等差数列,则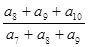 的值为
的值为


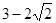
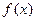 的图象经过点
的图象经过点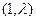 ,且对任意
,且对任意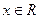 ,都有
,都有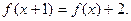 数列
数列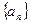 满足
满足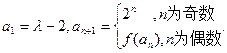
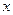 为正整数时,求
为正整数时,求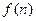 的表达式
的表达式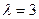 ,求
,求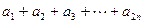
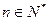 ,总有
,总有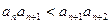 ,求实数
,求实数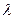 的取值范围
的取值范围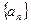
 满足前2项的和为5,前6项的和为3.
满足前2项的和为5,前6项的和为3.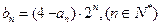 ,求数列
,求数列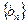 的前
的前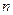 项和
项和