题目内容
在数列{an}中,a1=2,an+1=an+ln(1+
),则an=( )
),则an=( )| A．2+lnn | B．2+(n-1)lnn | C．2+nlnn | D．1+n+lnn |
A
【思路点拨】根据递推式采用“叠加”方法求解.
解:∵an+1=an+ln(1+)=an+ln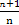
=an+ln(n+1)-lnn,
∴a2=a1+ln2,a3=a2+ln3-ln2,…,an=an-1+lnn-ln(n-1),
将上面n-1个式子左右两边分别相加得an=a1+ln2+(ln3-ln2)+(ln4-ln3)+…+[lnn-ln(n-1)]=a1+lnn=2+lnn.
解:∵an+1=an+ln(1+
)=an+ln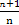=an+ln(n+1)-lnn,∴a2=a1+ln2,a3=a2+ln3-ln2,…,an=an-1+lnn-ln(n-1),
将上面n-1个式子左右两边分别相加得an=a1+ln2+(ln3-ln2)+(ln4-ln3)+…+[lnn-ln(n-1)]=a1+lnn=2+lnn.
练习册系列答案
阅读快车系列答案
相关题目
}中，已知
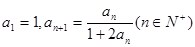
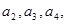并由此猜想数列{
的前n项和．
,an+1=1-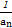
(n≥2),则a16= .
的前n项和Tn＝________．