题目内容
在等比数列{an}中,a6与a7的等差中项等于48,a4a5a6a7a8a9a10=1286.如果设数列{an}的前n项和为Sn,那么Sn=( )
| A.5n-4 | B.4n-3 |
| C.3n-2 | D.2n-1 |
D
设等比数列{an}的公比为q,由a6与a7的等差中项等于48,得a6+a7=96,即a1q5(1+q)=96. ①
由等比数列的性质,得a4a10=a5a9=a6a8=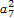 .
.
因为a4a5a6a7a8a9a10=1286,
则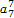 =1286=(26)7,即a1q6=26. ②
=1286=(26)7,即a1q6=26. ②
由①②解得a1=1,q=2,
∴Sn=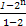 =2n-1,故选D.
=2n-1,故选D.
由等比数列的性质,得a4a10=a5a9=a6a8=
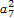 .
.因为a4a5a6a7a8a9a10=1286,
则
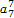 =1286=(26)7,即a1q6=26. ②
=1286=(26)7,即a1q6=26. ②由①②解得a1=1,q=2,
∴Sn=
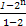 =2n-1,故选D.
=2n-1,故选D.
练习册系列答案
相关题目
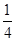
 +sinx的所有正的极小值点从小到大排成的数列为{xn}.
+sinx的所有正的极小值点从小到大排成的数列为{xn}. ),则an=( )
),则an=( )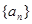 中,
中,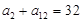 ,则
,则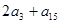 的值是( )
的值是( )