题目内容
已知函数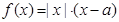 .
.
(I)判断 的奇偶性;
的奇偶性;
(Ⅱ)设函数 在区间
在区间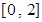 上的最小值为
上的最小值为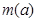 ,求
,求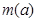 的表达式;
的表达式;
(Ⅲ)若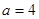 ,证明:方程
,证明:方程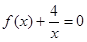 有两个不同的正数解.
有两个不同的正数解.
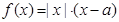 .
.(I)判断
 的奇偶性;
的奇偶性;(Ⅱ)设函数
 在区间
在区间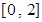 上的最小值为
上的最小值为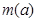 ,求
,求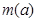 的表达式;
的表达式;(Ⅲ)若
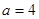 ,证明:方程
,证明:方程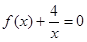 有两个不同的正数解.
有两个不同的正数解. (I) 既不是奇函数也不是偶函数
既不是奇函数也不是偶函数
(Ⅱ)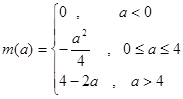 (Ⅲ)见解析
(Ⅲ)见解析
 既不是奇函数也不是偶函数
既不是奇函数也不是偶函数(Ⅱ)
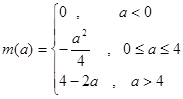 (Ⅲ)见解析
(Ⅲ)见解析(1)对参数a进行讨论,利用奇偶函数的定义,即可得出结论;
(2)当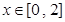 时,
时,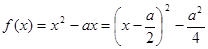 ,然后转化为二次函数轴动区间定的最值问题来研究即可.
,然后转化为二次函数轴动区间定的最值问题来研究即可.
(3)利用图像法,把方程根的个数转化为两个函数图像交点的个数来研究.
当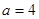 ,若
,若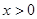 时,
时,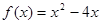 ,方程可化为
,方程可化为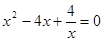 即
即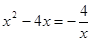 .
.
令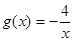 ,在同一直角坐标系中作出函数
,在同一直角坐标系中作出函数 ,
,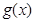 在
在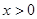 时的图像从图像确定函数
时的图像从图像确定函数 与
与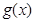 的图像在第四象限有两个不同交点,从而证明方程
的图像在第四象限有两个不同交点,从而证明方程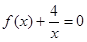 有两个不同的正数解.解:(I)
有两个不同的正数解.解:(I) 时,
时, 是奇函数;……(1分)
是奇函数;……(1分)
 时,
时, 既不是奇函数也不是偶函数.……(2分)
既不是奇函数也不是偶函数.……(2分)
(II)当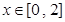 时,
时,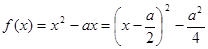 ,函数
,函数 图像的对称轴为直线
图像的对称轴为直线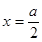 .(3分)
.(3分)
当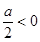 ,即
,即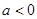 时,函数
时,函数 在
在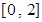 上是增函数,所以
上是增函数,所以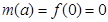 ;
;
当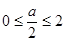 ,即
,即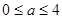 时,函数
时,函数 在
在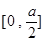 上是减函数,在
上是减函数,在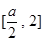 上是增函数,
上是增函数,
所以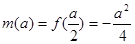 ;……(5分)
;……(5分)
当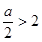 ,即
,即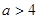 时,函数
时,函数 在
在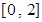 上是减函数,
上是减函数,
所以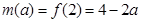 .……(6分)
.……(6分)
综上,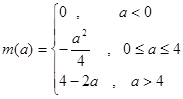 .……(7分)
.……(7分)
(III)证法一:
若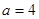 ,则
,则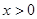 时,
时,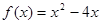 ,方程可化为
,方程可化为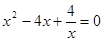 ,
,
即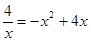 .……(8分)
.……(8分)
令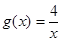 ,
,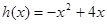 ,在同一直角坐标系中作出函数
,在同一直角坐标系中作出函数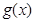
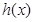 在
在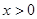 时的图像…(9分)
时的图像…(9分)

因为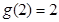 ,
,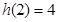 ,所以
,所以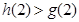 ,即当
,即当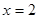 时
时
函数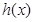 图像上的点在函数
图像上的点在函数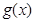 图像点的上方.……(11分)
图像点的上方.……(11分)
所以函数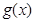 与
与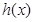 的图像在第一象限有两个不同交点.
的图像在第一象限有两个不同交点.
即方程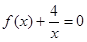 有两个不同的正数解.…………(12分)
有两个不同的正数解.…………(12分)
证法二:
若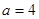 ,则
,则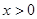 时,
时,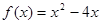 ,方程可化为
,方程可化为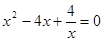 ,
,
即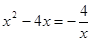 .…………(8分)
.…………(8分)
令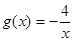 ,在同一直角坐标系中作出函数
,在同一直角坐标系中作出函数 ,
,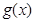 在
在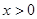 时的图像.(9分)
时的图像.(9分)
因为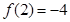 ,
,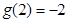 ,所以
,所以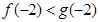 ,
,
即当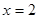 时,函数
时,函数 图像上的点在函数
图像上的点在函数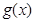 图像点的上方.…………(11分)
图像点的上方.…………(11分)
所以函数 与
与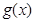 的图像在第四象限有两个不同交点.
的图像在第四象限有两个不同交点.
所以方程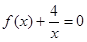 有两个不同的正数解.…………(12分)
有两个不同的正数解.…………(12分)
(2)当
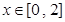 时,
时,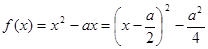 ,然后转化为二次函数轴动区间定的最值问题来研究即可.
,然后转化为二次函数轴动区间定的最值问题来研究即可.(3)利用图像法,把方程根的个数转化为两个函数图像交点的个数来研究.
当
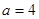 ,若
,若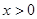 时,
时,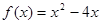 ,方程可化为
,方程可化为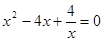 即
即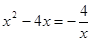 .
.
|
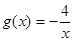 ,在同一直角坐标系中作出函数
,在同一直角坐标系中作出函数 ,
,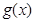 在
在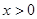 时的图像从图像确定函数
时的图像从图像确定函数 与
与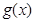 的图像在第四象限有两个不同交点,从而证明方程
的图像在第四象限有两个不同交点,从而证明方程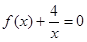 有两个不同的正数解.解:(I)
有两个不同的正数解.解:(I) 时,
时, 是奇函数;……(1分)
是奇函数;……(1分) 时,
时, 既不是奇函数也不是偶函数.……(2分)
既不是奇函数也不是偶函数.……(2分)(II)当
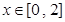 时,
时,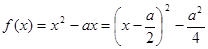 ,函数
,函数 图像的对称轴为直线
图像的对称轴为直线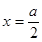 .(3分)
.(3分)当
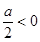 ,即
,即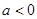 时,函数
时,函数 在
在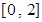 上是增函数,所以
上是增函数,所以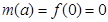 ;
;当
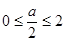 ,即
,即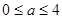 时,函数
时,函数 在
在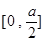 上是减函数,在
上是减函数,在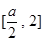 上是增函数,
上是增函数,所以
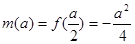 ;……(5分)
;……(5分)当
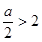 ,即
,即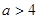 时,函数
时,函数 在
在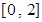 上是减函数,
上是减函数,所以
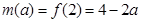 .……(6分)
.……(6分)综上,
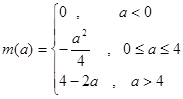 .……(7分)
.……(7分)(III)证法一:
若
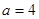 ,则
,则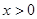 时,
时,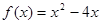 ,方程可化为
,方程可化为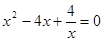 ,
,即
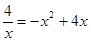 .……(8分)
.……(8分)令
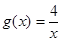 ,
,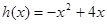 ,在同一直角坐标系中作出函数
,在同一直角坐标系中作出函数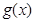
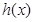 在
在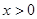 时的图像…(9分)
时的图像…(9分)
因为
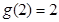 ,
,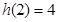 ,所以
,所以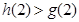 ,即当
,即当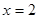 时
时函数
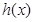 图像上的点在函数
图像上的点在函数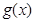 图像点的上方.……(11分)
图像点的上方.……(11分)所以函数
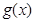 与
与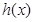 的图像在第一象限有两个不同交点.
的图像在第一象限有两个不同交点.即方程
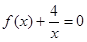 有两个不同的正数解.…………(12分)
有两个不同的正数解.…………(12分)证法二:
若
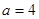 ,则
,则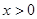 时,
时,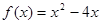 ,方程可化为
,方程可化为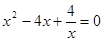 ,
,即
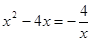 .…………(8分)
.…………(8分)
|
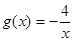 ,在同一直角坐标系中作出函数
,在同一直角坐标系中作出函数 ,
,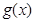 在
在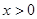 时的图像.(9分)
时的图像.(9分)
因为
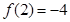 ,
,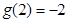 ,所以
,所以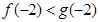 ,
,即当
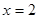 时,函数
时,函数 图像上的点在函数
图像上的点在函数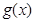 图像点的上方.…………(11分)
图像点的上方.…………(11分)所以函数
 与
与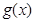 的图像在第四象限有两个不同交点.
的图像在第四象限有两个不同交点.所以方程
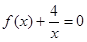 有两个不同的正数解.…………(12分)
有两个不同的正数解.…………(12分)
练习册系列答案
相关题目
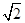 ]上的最小值.
]上的最小值.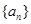 中,
中,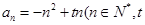 为常数),且
为常数),且
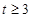
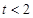
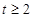
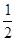 )=0,则不等式f(log4x)>0的解集是______________.
)=0,则不等式f(log4x)>0的解集是______________.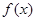 在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则函数
在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则函数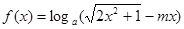 在R上为奇函数,
在R上为奇函数,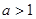 ,
,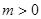 .
.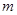 的值;
的值;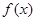 的单调性.(不需要证明)
的单调性.(不需要证明)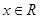 ,都有
,都有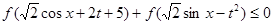 ;是否存在
;是否存在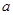 的值,使
的值,使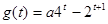 最小值为
最小值为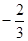 ;
;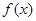 的定义域为
的定义域为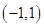 ,且同时满足下列条件:
,且同时满足下列条件: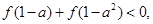 求
求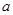 的取值范围。
的取值范围。 )=f(x)-f(y).
)=f(x)-f(y). )<2.
)<2.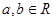 ,记
,记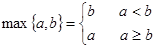 ,若函数
,若函数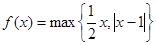 ,其中
,其中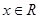 ,则
,则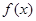 的最小值为 .
的最小值为 .