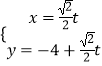题目内容
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,且![]()
(1)判断△ABC的形状,并加以证明;
(2)当c = 1时,求△ABC周长的最大值.
【答案】(1)见解析;(2)ABC周长的最大值为 ![]()
.
【解析】试题分析:(1)由![]() 可得:
可得: ![]() 即cosA=
即cosA=![]() ,即b=c×cosA
,即b=c×cosA
由余弦定理得: ![]() ∴c2=a2+b2即得三角形形状(2)由(1)知△ABC为直角三角形,c为斜边,当c=1时设另两直角边长分别为a,b,则a2+b2=1 ∵
∴c2=a2+b2即得三角形形状(2)由(1)知△ABC为直角三角形,c为斜边,当c=1时设另两直角边长分别为a,b,则a2+b2=1 ∵![]() ∴△ABC周长=1+a+b
∴△ABC周长=1+a+b![]() 即得△ABC周长的最大值.
即得△ABC周长的最大值.
试题解析:
(1)原式可得: ![]()
即cosA=![]() 即b=c×cosA
即b=c×cosA
由余弦定理得: ![]()
∴c2=a2+b2 即△ABC为直角三角形
(2)由(1)知△ABC为直角三角形,c为斜边
当c=1时设另两直角边长分别为a,b
a2+b2=1
∵![]()
∴△ABC周长=1+a+b![]()
当且仅当a=b即 △ABC为等腰直角三角形时取等号.
∴△ABC周长的最大值为 ![]()

【题目】某农场共有土地50亩,这些地可种西瓜、棉花、玉米.这些农作物每亩地所需劳力和预计产值如下表.若该农场有20名劳动力,应怎样计划才能使每亩地都能种上作物(玉米必种),所有劳动力都被安排工作(每名劳动力只能种植一种作物)且作物预计总产值达最高?
作物 | 劳力/亩 | 产值/亩 |
西瓜 | 1/2 | 0.6万元 |
棉花 | 1/3 | 0.5万元 |
玉米 | 1/4 | 0.3万元 |
【题目】“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801﹣2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
累积净化量(克) | (3,5] | (5,8] | (8,12] | 12以上 |
等级 | P1 | P2 | P3 | P4 |
为了了解一批空气净化器(共2000台)的质量,随机抽取n台机器作为样本进行估计,已知这n台机器的
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率.