题目内容
【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,nSn+1﹣(n+1)Sn= ![]() ,n∈N*
,n∈N*
(1)求a2的值;
(2)求数列{an}的通项公式.
【答案】
(1)解:由a1=1,nSn+1﹣(n+1)Sn= ![]() ,n∈N*,令n=1,则S2﹣2S1=1,
,n∈N*,令n=1,则S2﹣2S1=1,
∴a2+1﹣2=1,解得a2=2
(2)解:由nSn+1﹣(n+1)Sn= ![]() ,n∈N*,变形为:
,n∈N*,变形为: ![]() =
= ![]() ,
,
∴数列 ![]() 是等差数列,首项为1,公差为
是等差数列,首项为1,公差为 ![]() .
.
∴ ![]() =1+
=1+ ![]() =
= ![]() ,
,
∴Sn= ![]() ,
,
∴当n≥2时,Sn﹣1= ![]() ,
,
an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =n,
=n,
∴an=n.
【解析】(1)由a1=1,nSn+1﹣(n+1)Sn= ![]() ,n∈N*,令n=1,解出即可.(2)由nSn+1﹣(n+1)Sn=
,n∈N*,令n=1,解出即可.(2)由nSn+1﹣(n+1)Sn= ![]() ,n∈N*,变形为:
,n∈N*,变形为: ![]() =
= ![]() ,利用等差数列的通项公式可得
,利用等差数列的通项公式可得 ![]() ,再利用Sn与an的关系即可得出.
,再利用Sn与an的关系即可得出.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
= 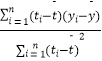 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.