题目内容
【题目】已知扇形的周长为30，当它的半径R和圆心角α各取何值时，扇形的面积S最大？并求出扇形面积的最大值．
【答案】当扇形半径为
，圆心角为2时，扇形有最大面积
．
【解析】试题分析：根据条件扇形的周长为30可以得到l+2R=30,从而扇形的面积S=
lR=（30－2R）R=
，即把S表示为R的二次函数，根据二次函数求最值的方法，可以进一步变形为
S=－（R－
）2+
，从而得到当扇形半径为，圆心角为2时，扇形有最大面积．
∵扇形的周长为30，∴l+2R=30，l=30-2R，
∴S=lR=（30－2R）R=
=－（R－）2+．．．．．5分
∴当R=时，扇形有最大面积，此时l=30－2R=15， 
=
=2．．．．．．．．8分
答：当扇形半径为，圆心角为2时，扇形有最大面积．．．．．10分．
名校通行证有效作业系列答案
【题目】为了解喜好体育运动是否与性别有关，某报记者随机采访50个路人，将调查情况进行整理后制成下表：
年龄（岁） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75） |
频数 | 5 | 10 | 8 | 10 | 5 | 5 |
喜好人数 | 4 | 6 | 6 | 3 | 3 |
（1）在调查的结果中，喜好体育运动的女性有10人，不喜好体育运动的男性有5人，请将下面的2×2列联表补充完整，并判断能否在犯错误的概率不超过0.005的前提下认为喜好体育运动与性别有关？说明你的理由；
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
（2）若从年龄在[15，25），[25，35）的被调查者中各随机选取两人进行追踪调查，记选中的4人中不喜好体育运动的人数为X，求随机变量X的分布列和数学期望． 下面的临界值表供参考：
P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：K2= 
，其中n=a+b+c+d）
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入（单位：万元）的数据如下表：
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（Ⅰ）求y关于x的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，分析2010年至2016年该村人均纯收入的变化情况，并预测该村2017年人均纯收入．
附：回归直线的斜率和截距的最小乘法估计公式分别为： 
= 
， 
= 
﹣ 
．
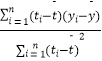