题目内容
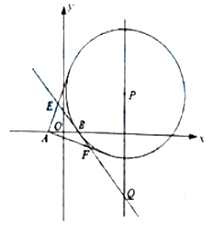
【题目】已知在直角坐标系xOy中,曲线C1的参数方程为 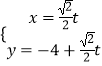 (t为参数),在极坐标系(以坐标原点O为极点,x轴的正半轴为极轴)中,曲线C2的方程为ρsin2θ=2pcosθ(p>0),曲线C1、C2交于A、B两点.
(t为参数),在极坐标系(以坐标原点O为极点,x轴的正半轴为极轴)中,曲线C2的方程为ρsin2θ=2pcosθ(p>0),曲线C1、C2交于A、B两点.
(Ⅰ)若p=2且定点P(0,﹣4),求|PA|+|PB|的值;
(Ⅱ)若|PA|,|AB|,|PB|成等比数列,求p的值.
【答案】解:(Ⅰ)∵曲线C2的方程为ρsin2θ=2pcosθ(p>0),即为ρ2sin2θ=2pρcosθ(p>0),
∴曲线C2的直角坐标方程为y2=2px,p>2.
又已知p=2,∴曲线C2的直角坐标方程为y2=4x.
将曲线C1的参数方程 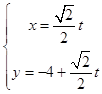 (t为参数)与y2=4x联立得:
(t为参数)与y2=4x联立得: ![]() t+32=0,
t+32=0,
由于△= ![]() ﹣4×32>0,
﹣4×32>0,
设方程两根为t1,t2,
∴t1+t2=12 ![]() ,t1t2=32,
,t1t2=32,
∴|PA|+|PB|=|t1|+|t2|=|t1+t2|=12 ![]() .
.
(Ⅱ)将曲线C1的参数方程 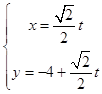 (t为参数)与y2=2px联立得:t2﹣2
(t为参数)与y2=2px联立得:t2﹣2 ![]() (4+p)t+32=0,
(4+p)t+32=0,
由于△= ![]() ﹣4×32=8(p2+8p)>0,
﹣4×32=8(p2+8p)>0,
∴t1+t2=2 ![]() (4+p),t1t2=32,
(4+p),t1t2=32,
又|PA|,|AB|,|PB|成等比数列,
∴|AB|2=|PA||PB,
∴ ![]() =|t1||t2|,
=|t1||t2|,
∴ ![]() =5t1t2,
=5t1t2,
∴ ![]() =5×32,
=5×32,
∴p2+8p﹣4=0,解得:p=﹣4 ![]() ,
,
又p>0,
∴p=﹣4+2 ![]() ,
,
∴当|PA|,|AB|,|PB|成等比数列时,p的值为﹣4+2 ![]()
【解析】(Ⅰ)曲线C2的方程为ρsin2θ=2pcosθ(p>0),即为ρ2sin2θ=2pρcosθ(p>0),利用互化公式可得直角坐标方程.将曲线C1的参数方程 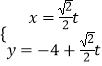 (t为参数)与抛物线方程联立得:
(t为参数)与抛物线方程联立得: ![]() t+32=0,可得|PA|+|PB|=|t1|+|t2|=|t1+t2|.(Ⅱ)将曲线C1的参数方程与y2=2px联立得:t2﹣2
t+32=0,可得|PA|+|PB|=|t1|+|t2|=|t1+t2|.(Ⅱ)将曲线C1的参数方程与y2=2px联立得:t2﹣2 ![]() (4+p)t+32=0,又|PA|,|AB|,|PB|成等比数列,可得|AB|2=|PA||PB|,可得
(4+p)t+32=0,又|PA|,|AB|,|PB|成等比数列,可得|AB|2=|PA||PB|,可得 ![]() =|t1||t2|,即
=|t1||t2|,即 ![]() =5t1t2,利用根与系数的关系即可得出.
=5t1t2,利用根与系数的关系即可得出.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】执行如图所示的程序框图,则下列说法正确的( ) 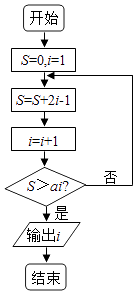
A.a∈(2,4),输出的i的值为5
B.a∈(4,5),输出的i的值为5
C.a∈(3,4),输出的i的值为5
D.a∈(2,4),输出的i的值为5
【题目】为了解喜好体育运动是否与性别有关,某报记者随机采访50个路人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 8 | 10 | 5 | 5 |
喜好人数 | 4 | 6 | 6 | 3 | 3 |
(1)在调查的结果中,喜好体育运动的女性有10人,不喜好体育运动的男性有5人,请将下面的2×2列联表补充完整,并判断能否在犯错误的概率不超过0.005的前提下认为喜好体育运动与性别有关?说明你的理由;
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不喜好体育运动的人数为X,求随机变量X的分布列和数学期望. 下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)