题目内容
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 ![]() 与p,且乙投球2次均未命中的概率为
与p,且乙投球2次均未命中的概率为 ![]() .
.
(Ⅰ)求乙投球的命中率p;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为ξ,求ξ的分布列和数学期望.
【答案】解:(Ⅰ)根据乙投球2次均未命中的概率为 ![]() ,两次是否投中相互之间没有影响,
,两次是否投中相互之间没有影响,
设“甲投球一次命中”为事件A,“乙投球一次命中”为事件B
由题意得 ![]()
解得 ![]() 或
或 ![]() (舍去),
(舍去),
∴乙投球的命中率为 ![]() .
.
(Ⅱ)由题设和(Ⅰ)知 ![]()
ξ可能的取值为0,1,2,3,
![]()
P(ξ=1)=P(A)P( ![]() )+
)+ ![]() P(B)P(
P(B)P( ![]() )P(
)P( ![]() )=
)= ![]()
![]()
![]()
∴ξ的分布列为
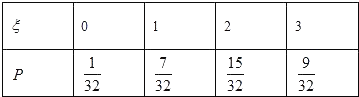
∴ξ的数学期望 ![]()
【解析】(Ⅰ)根据乙投球2次均未命中的概率为 ![]() ,两次是否投中相互之间没有影响,根据相互独立事件的概率公式写出乙两次都未投中的概率,列出方程,解方程即可.(II)做出甲投球命中的概率和乙投球命中的概率,因为两人共命中的次数记为ξ,得到变量可能的取值,看清楚变量对应的事件,做出事件的概率,写出分布列和期望.
,两次是否投中相互之间没有影响,根据相互独立事件的概率公式写出乙两次都未投中的概率,列出方程,解方程即可.(II)做出甲投球命中的概率和乙投球命中的概率,因为两人共命中的次数记为ξ,得到变量可能的取值,看清楚变量对应的事件,做出事件的概率,写出分布列和期望.
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

【题目】执行如图所示的程序框图,则下列说法正确的( ) 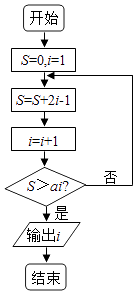
A.a∈(2,4),输出的i的值为5
B.a∈(4,5),输出的i的值为5
C.a∈(3,4),输出的i的值为5
D.a∈(2,4),输出的i的值为5
【题目】为了考察某种中成药预防流感的效果,抽样调查40人,得到如下数据
| 患流感 | 未患流感 |
服用药 | 2 | 18 |
未服用药 | 8 | 12 |
根据表中数据,通过计算统计量K2= ![]() ,并参考以下临界数据:
,并参考以下临界数据:
P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
若由此认为“该药物有效”,则该结论出错的概率不超过( )
A.0.05
B.0.025
C.0.01
D.0.005