��Ŀ����
����Ŀ����߹������ŵij���ͨ�еij���ͨ�������ɸ����������еĽ�ͨ״������һ������£������ϵij����ٶ�![]() ����λ��ǧ��/Сʱ���dz����ܶ�
����λ��ǧ��/Сʱ���dz����ܶ�![]() ����λ����/ǧ�ף�
����λ����/ǧ�ף�
�ĺ����������ϵij����ܶȴﵽ200��/ǧ��ʱ���ͻ���ɶ�������ʱ�����ٶ�Ϊ0����
�����ܶȲ�����20��/ǧ��ʱ�������ٶ�Ϊ60ǧ��/Сʱ���о���������![]() ʱ��
ʱ��
�����ٶ�![]() �dz����ܶ�
�dz����ܶ�![]() ��һ�κ�����
��һ�κ�����
��1����![]() ʱ������
ʱ������![]() �ı���ʽ��
�ı���ʽ��
��2���������������λʱ����ͨ������ij�۲��ij�������![]() (��λ����/Сʱ��,��ô�������ܶ�
(��λ����/Сʱ��,��ô�������ܶ�![]() Ϊ���ʱ��������
Ϊ���ʱ��������![]() ���Դﵽ���������ֵ������ȷ��
���Դﵽ���������ֵ������ȷ��![]() ��/Сʱ��.
��/Сʱ��.
���𰸡���1��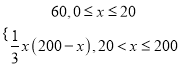 ����2��
����2��![]()
![]() .
.
�����������������
���⿼�麯��ģ����ʵ���е�Ӧ���Լ��ֶκ�����ֵ������1�����������÷ֶκ�������ϴ���ϵ������������Ĺ�ϵʽ����2������������õ�![]() �Ľ���ʽ���ٸ��ݷֶκ�����ֵ����������ֵ���ɡ�
�Ľ���ʽ���ٸ��ݷֶκ�����ֵ����������ֵ���ɡ�
���������
(1)������:��![]() ʱ,
ʱ, ![]() ;
;
��![]() ʱ,��
ʱ,��![]()
����֪��![]() ���
���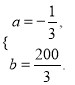
��![]() ��
��
���Ͽɵ�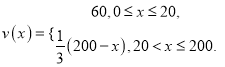
(2)�����Ⲣ�ɣ�1���ɵ�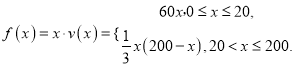
�ٵ�![]() ʱ��
ʱ�� ![]() Ϊ��������
��������
�൱![]() ʱ��
ʱ�� ![]() ȡ�����ֵ�������ֵΪ
ȡ�����ֵ�������ֵΪ![]() 1200 ��
1200 ��
�ڵ�![]() ʱ��
ʱ�� ![]() ��
��
�൱![]() ʱ��
ʱ�� ![]() ȡ�����ֵ�������ֵΪ
ȡ�����ֵ�������ֵΪ![]() ��
��
����![]() �����ֵΪ
�����ֵΪ![]() ��
��
�ʵ������ܶ�Ϊ100��/ǧ��ʱ�����������Դﵽ����Ҵ�ֵΪ3333��/Сʱ.

 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�����Ŀ������лƺ�̲��ij��2010����2016���˾������루��λ����Ԫ�����������±���
��� | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
��ݴ���x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�˾�������y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
������y����x�����Իع鷽�̣�
�������ã����еĻع鷽�̣�����2010����2016��ô��˾�������ı仯�������Ԥ��ô�2017���˾������룮
�����ع�ֱ�ߵ�б�ʺͽؾ����С�˷����ƹ�ʽ�ֱ�Ϊ�� ![]() =
= 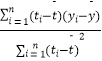 ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
����Ŀ��Ϊ�˿���ij���г�ҩԤ�����е�Ч������������40�ˣ��õ���������
| ������ | ����� |
����ҩ | 2 | 18 |
δ����ҩ | 8 | 12 |
���ݱ������ݣ�ͨ������ͳ����K2= ![]() �����ο������ٽ����ݣ�
�����ο������ٽ����ݣ�
P��K2��k0�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
���ɴ���Ϊ����ҩ����Ч������ý��۳����ĸ��ʲ������� ��
A.0.05
B.0.025
C.0.01
D.0.005