题目内容
【题目】已知函数f(x),定义 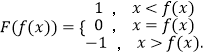
(Ⅰ)写出函数F(2x﹣1)的解析式;
(Ⅱ)若F(|x﹣a|)+F(2x﹣1)=0,求实数a的值;
(Ⅲ)当 ![]() 时,求h(x)=cosxF(x+sinx)的零点个数和值域.
时,求h(x)=cosxF(x+sinx)的零点个数和值域.
【答案】解:(Ⅰ)定义 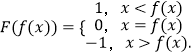 ,
,
当2x﹣1>x,可得x>1,则F(2x﹣1)=1;
当2x﹣1=x,可得x=1,则F(2x﹣1)=0;
当2x﹣1<x,可得x<1,则F(2x﹣1)=﹣1;
可得F(2x﹣1)= 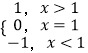 ;
;
(Ⅱ)当x>1时,F(2x﹣1)=1,F(|x﹣a|)=﹣1,
即有|x﹣a|<x恒成立,即为a2≤2ax在x>1恒成立,
即有a2≤2a,解得0≤a≤2;
当x=1时,F(2x﹣1)=0,F(|x﹣a|)=0,
可得|1﹣a|=1,解得a=0或2;
当x<1时,F(2x﹣1)=﹣1,F(|x﹣a|)=1,
即有|x﹣a|>x恒成立,即为a2≥2ax在x<1恒成立,
即有a2≥2a,解得a≥2或a≤0;
则a的值为0或2;
(Ⅲ)当 ![]() 时,h(x)=cosxF(x+sinx)=0,
时,h(x)=cosxF(x+sinx)=0,
可得cosx=0或F(x+sinx)=0,
即有x= ![]() ;x+sinx=x,即sinx=0,解得x=π,
;x+sinx=x,即sinx=0,解得x=π,
则h(x)的零点个数为2;
当x+sinx>x,即 ![]() ≤x<π时,h(x)=cosx∈(﹣1,
≤x<π时,h(x)=cosx∈(﹣1, ![]() ];
];
当x+sinx=x,即x=π时,h(x)=0;
当x+sinx<x,即π<x≤ ![]() 时,h(x)=﹣cosx∈[
时,h(x)=﹣cosx∈[ ![]() ,1).
,1).
综上可得,h(x)的值域为(﹣1,1).
【解析】根据分段函数的定义,讨论2x-1所在的区间,从而得到F(2x-1)的解析式,(2)对x进行讨论,由F(2x-1)求得F(|x﹣a|),运用恒成立思想,即可得到a的值,(3)当h(x)=0时,可得cosx=0或F(x+sinx)=0,对x+sinx进行讨论,在相应的区间内求得值域,综上得到h(x)的值域.

【题目】某市家庭煤气的使用量x(m3)和煤气费f(x)(元) 满足关系f(x)= ![]() ,已知某家庭今年前三个月的煤气费如表:
,已知某家庭今年前三个月的煤气费如表:
月份 | 用气量 | 煤气费 |
一月份 | 4m3 | 4 元 |
二月份 | 25m3 | 14 元 |
三月份 | 35m3 | 19 元 |
若四月份该家庭使用了20m3的煤气,则其煤气费为( )元.
A.10.5
B.10
C.11.5
D.11
【题目】某产品在某销售点的零售价x(单位:元)与每天的销售量y(单位:个)的统计数据如表所示:
x | 16 | 17 | 18 | 19 |
y | 50 | 34 | 41 | 31 |
由表可得回归直线方程 ![]() 中的
中的 ![]() ,根据模型预测零售价为20元时,每天的销售量约为( )
,根据模型预测零售价为20元时,每天的销售量约为( )
A.30
B.29
C.27.5
D.26.5