Question

【题目】已知函数f（x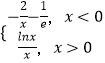）= 若关于x的方程f（x）=t有三个不同的解，其中最小的解为a，则 的取值范围为 ．

Answer 1

【答案】
【解析】解：当x＜0时，f（x）为增函数，且当x→﹣∞时，f（x）→﹣ ．

当x＞0时，f′（x）= ，

∴当0＜x＜e时，f′（x）＞0，f（x）单调递增，

当x＞e时，f′（x）＜0，f（x）单调递减，

又当x→0时，f（x）→﹣∞，当x→+∞时，f（x）→0，

∴当x=e时，f（x）取得极大值f（e）= ．

作出f（x）在定义域的函数图象如图所示：

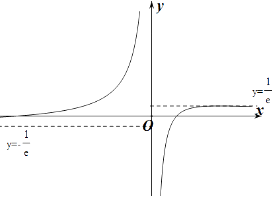
∵f（x）=t有三解，∴0 ，

令﹣ =t得x=﹣ ，即a=﹣ ，

∴ =﹣ ﹣ ，

令g（t）=﹣ ﹣ ，则g（t）在（0， ）上单调递减，

∴﹣ ＜g（t）＜0．

所以答案是： ．