题目内容
【题目】如图，在△ABC所在平面外有一点P，D，E分别是PB与AB上的点，过D，E作平面平行于BC，试画出这个平面与其他各面的交线，并说明画法的依据.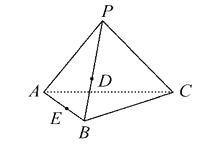
【答案】解：记过D，E所作平面为α，因为BC∥α，且BC 
平面PBC，BC 平面ABC，所以平面α与平面PBC和平面ABC的交线都与BC平行.
据此作平面α如下：连接DE，过点D作DG∥BC交PC于点G，
过点E作EF∥BC交AC于点F，连接GF，平面DEFG即为平面α.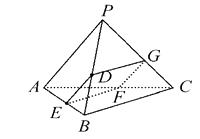
【解析】要使BC与所作的平面平行，由线面平行的性质得BC必与交线平行。
【考点精析】认真审题，首先需要了解直线与平面平行的性质(一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行)．
练习册系列答案
相关题目
