题目内容
【题目】已知椭圆C： 
的右焦点为F（1，0），点P是椭圆C上一动点，若动点P到点的距离的最大值为b2 ．
（1）求椭圆C的方程，并写出其参数方程；
（2）求动点P到直线l：x+2y﹣9=0的距离的最小值．
【答案】
（1）解：由题意右焦点为F（1，0），点P是椭圆C上一动点，
若动点P到点的距离的最大值为b2．
有： 
，
解得：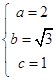 
，
∴椭圆C的方程为 
，其参数方程为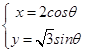 
（θ为参数）
（2）解：设点P坐标为 
，
则P到直线l：x+2y﹣9=0的距离
，
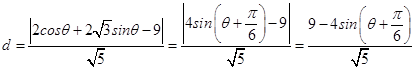∴当 
，即θ=2kπ+ 
，k∈Z时， 
，
∴动点P到直线l：x+2y﹣9=0的距离的最小值为 
【解析】（1）由椭圆的焦点坐标，可得c，再由椭圆上的点与焦点的距离最大值为a+c，解方程可得a，b，进而得到椭圆的方程和参数方程；（2）设点P坐标为 
，运用点到直线的距离公式，以及两角和的正弦公式，化简可得距离d，再由正弦函数的值域，可得最小值．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
相关题目
