题目内容
已知a>0,b>0,且2a+b=1,则S=2
-4a2-b2的最大值为 .
-4a2-b2的最大值为 .
因为a>0,b>0,2a+b=1,
所以4a2+b2=(2a+b)2-4ab=1-4ab,
且1=2a+b≥2
,即≤
,ab≤
,
所以S=2-4a2-b2=2-(1-4ab)=2+4ab-1≤,当且仅当a=
,b=
时,等号成立.
所以4a2+b2=(2a+b)2-4ab=1-4ab,
且1=2a+b≥2
,即≤,ab≤,所以S=2
-4a2-b2=2-(1-4ab)=2+4ab-1≤,当且仅当a=,b=时,等号成立.
练习册系列答案
相关题目
+
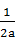,B=
(a>0,b>0),则A,B的大小关系为 .
,则两边均含有运算“*”和“+”,且对任意3个实数a,b,c都能成立的一个等式可以是 .
,Q=
,则P与Q的大小关系是 ( )
<
;②a2>b2;③
>
;④a|c|>b|c|.
，若“
”是“
”的充分条件，则
的取值范围是（ ）
>
,则实数x的取值范围是 ( )