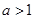题目内容
设x,y,z∈R+且x+y+z=6,则lgx+lgy+lgz的取值范围是 ( )
| A.(-∞,lg6] | B.(-∞,3lg2] |
| C.[lg6,+∞) | D.[3lg2,+∞) |
B
选B.因为x,y,z∈R+,
所以6=x+y+z≥3
 ,即xyz≤8,
,即xyz≤8,所以lgx+lgy+lgz=lgxyz≤lg8=3lg2.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 -4a2-b2的最大值为 .
-4a2-b2的最大值为 . ,则下列推证中正确的是( )
,则下列推证中正确的是( )



 ·
· ·
· ,则必有 ( )
,则必有 ( )

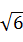
 恒成立,则实数a的取范围是( )
恒成立,则实数a的取范围是( )