Question

13．如图所示，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，底面边长为a，E是PC的中点．
（1）求证：PA∥面BDE；平面PAC⊥平面BDE；
（2）若二面角E-BD-C为30°，求四棱锥P-ABCD的体积．

Answer 1

分析 （1）连结EO，证明PA∥EO，可得PA∥面BDE；证明BD⊥平面PAC，可得平面PAC⊥平面BDE；
（2）求出四棱锥的高，即可求四棱锥P-ABCD的体积．

解答 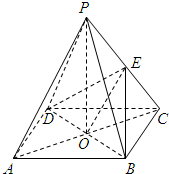（1）证明：连结EO
∵四边形ABCD是正方形，O是正方形的中心
∴BD⊥AC=O，AO=CO
∵在△PAC中，E为PC的中点，∴PA∥EO
又∵EO?平面BDE，PA?平面BDE
∴PA∥平面BDE；
∵PO⊥底面ABCD，BD?平面ABCD
∴PO⊥BD
又∵BD⊥AC，AC∩PO=E，PO?平面PAC，AC?平面PAC
∴BD⊥平面PAC
又∵BD?平面BDE
∴平面PAC⊥平面BDE；
（2）解：由（1）可知，∠EOC=30°，∴∠OPC=60°，
∵底面边长为a，
∴CO=$\frac{\sqrt{2}}{2}$a，
∴PO=$\frac{\sqrt{6}}{6}$a，
∴四棱锥P-ABCD的体积=$\frac{1}{3}{a}^{2}•\frac{\sqrt{6}}{6}a$=$\frac{\sqrt{6}}{18}{a}^{3}$．

点评 本题考查线面平行，平面与平面垂直的判定，考查四棱锥P-ABCD的体积，考查学生分析解决问题的能力，属于中档题．