题目内容
3．已知f（x）=x2-2x+a，若f（x）≥2恒成立，则a的取值范围是a≥3．分析 问题转化为x2-2x+a-2≥0对x∈R恒成立，只需△=22-4（a-2）≤0，解出即可．
解答 解：不等式f（x）≥2对x∈R恒成立，
等价于x2-2x+a-2≥0对x∈R恒成立，
则只需△=22-4（a-2）≤0即可，
解得：a≥3，
故答案为：a≥3．
点评 本题考查了二次函数的性质问题，考查转化思想，是一道基础题．
练习册系列答案
相关题目
13．函数y=ecosx（-π≤x≤π）的大致图象为（ ）
| A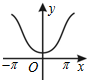． |  | B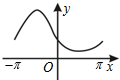． |  | C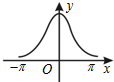． |  | D． |  |
14．定义集合A与B的运算：A⊙B={x|x∈A或x∈B，且x∉A∩B}，已知集合A={1，2，3，4}，B={3，4，5，6，7}，则（A⊙B）⊙B为（ ）
| A． | {1，2，3，4，5，6，7} | B． | {1，2，3，4} | C． | {1，2} | D． | {3，4，5，6，7} |
如图所示，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，底面边长为a，E是PC的中点．