题目内容
4.求函数f(x)=x4-3x2的值域.分析 令x2=t(t≥0)换元,然后借助于二次函数的性质求得最小值,则值域可求.
解答 解:令x2=t(t≥0),
则原函数化为g(t)=t2-3t(t≥0),
其对称轴方程为t=$\frac{3}{2}$,
∴当t=$\frac{3}{2}$时函数取得最小值为$(\frac{3}{2})^{2}-3×\frac{3}{2}=-\frac{9}{4}$.
∴函数f(x)=x4-3x2的值域为[-$\frac{9}{4},+∞$).
点评 本题考查函数值域的求法,训练了换元法和配方法求函数的值域,是基础题.

练习册系列答案
相关题目
14.定义集合A与B的运算:A⊙B={x|x∈A或x∈B,且x∉A∩B},已知集合A={1,2,3,4},B={3,4,5,6,7},则(A⊙B)⊙B为( )
| A. | {1,2,3,4,5,6,7} | B. | {1,2,3,4} | C. | {1,2} | D. | {3,4,5,6,7} |
9.集合A={x|(x-a)2≤1},B={x|(x-b)2≥9},A∪B=B,则( )
| A. | (a+b)2≥16 | B. | (a+b)2≤16 | C. | (a-b)2≥16 | D. | (a-b)2≤16 |
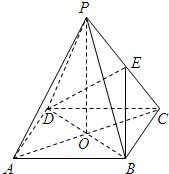 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.