Question

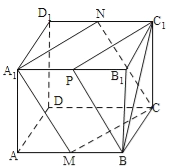
【题目】如图所示，在棱长为2的正方体中，的中点是P，过点作与截面平行的截面，则截面的面积为__________.

Answer 1

【答案】

【解析】

试题取AB、C1D1的中点M、N，连结A1M、MC、CN、NA1．由已知得四边形A1MCN是平行四边形，连结MN，作A1H⊥MN于H，由题意能求出截面的面积．

解：取AB、C1D1的中点M、N，连结A1M、MC、CN、NA1．

由于A1N∥PC1∥MC且A1N=PC1=MC，

∴四边形A1MCN是平行四边形．

又∵A1N∥PC1，A1M∥BP，A1N∩A1M=A1，

PC1∩BP=P，

∴平面A1MCN∥平面PBC1

因此，过A1点作与截面PBC1平行的截面是平行四边形．

又连结MN，作A1H⊥MN于H，由于A1M=A1N=，MN=2，

则AH=．

∴=，

故=2=2．

故答案为．