Question

【题目】如图，在四棱锥P－ABCD中，底面ABCD是菱形，∠ADC＝60°，侧面PDC是正三角形，平面PDC⊥平面ABCD，CD＝2，M为PB的中点.

(1)求证：PA⊥平面CDM．

(2)求二面角D－MC－B的余弦值．

Answer 1

【答案】(1) 见解析；(2)－．

【解析】试题分析：

（1）取DC中点O，连接PO，根据题意可证得OA，OC，OP两两垂直，建立空间直角坐标系，运用坐标法可证得，从而PA⊥DM，PA⊥DC，根据线面垂直的判定定理可得结论．（2）结合（1）可求得平面BMC的一个法向量，又平面CDM的法向量为，求出两向量夹角的余弦值，结合图形可得二面角的余弦值．

试题解析：

（1）取DC中点O，连接PO．

∵侧面PDC是正三角形，

∴PO⊥DC，

又平面PDC⊥平面ABCD，平面PDC∩平面ABCD＝DC，

∴PO⊥底面ABCD．

又底面ABCD为菱形，且∠ADC＝60°，DC＝2，

∴DO＝1，OA⊥DC．

以O为原点，分别以OA，OC，OP所在直线为x轴，y轴，z轴，建立如图所示的空间直角坐标系O-xyz．

则， ，

∴，

∴，

∴PA⊥DM，PA⊥DC，

又DM∩DC＝D，

∴PA⊥平面CDM．

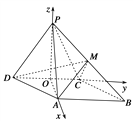
(2)由（1）得，

设平面BMC的一个法向量，

由，得，

令z＝1，得．

由(1)知平面CDM的法向量为，

∴，

由图形知二面角D－MC－B是钝角，

所以二面角D－MC－B的余弦值为．