题目内容
【题目】设a,b∈R,关于x的方程(x2﹣ax+1)(x2﹣bx+1)=0的四个实根构成以q为公比的等比数列,若q∈[![]() ,2],则ab的取值范围为______.
,2],则ab的取值范围为______.
【答案】![]() .
.
【解析】
利用等比数列的性质确定方程的根,由韦达定理表示出ab,再利用换元法转化为二次函数,根据q的范围和二次函数的性质,确定ab的最值即可求出ab的取值范围.
解:设方程(x2﹣ax+1)(x2﹣bx+1)=0的4个实数根依次为m,mq,mq2,mq3,
由等比数列性质,不妨设m,mq3为x2﹣ax+1=0的两个实数根,则mq,mq2为方程x2﹣bx+1=0的两个根,
由韦达定理得,m2q3=1,m+mq3=a,mq+mq2=b,则![]()
故ab=(m+mq3)(mq+mq2)=m2(1+q3)(q+q2)
![]() (1+q3)(q+q2)
(1+q3)(q+q2)![]() ,
,
设t![]() ,则
,则![]() t2﹣2,
t2﹣2,
因为q∈[![]() ,2],且t
,2],且t![]() 在[
在[![]() ,1]上递减,在(1,2]上递增,
,1]上递减,在(1,2]上递增,
所以t∈[2,![]() ],
],
则ab=t2+t﹣2![]() ,
,
所以当t=2时,ab取到最小值是4,
当t![]() 时,ab取到最大值是
时,ab取到最大值是![]() ,
,
所以ab的取值范围是:![]() .
.

 阶梯计算系列答案
阶梯计算系列答案【题目】2019年10月5日, 美国NBA火箭队总经理莫雷公开发布涉港错误言论,中国公司与明星纷纷站出来抵制火箭队,随后京东、天猫、淘宝等中国电商平台全线下架了火箭队的所有商品,当天有大量网友关注此事,某网上论坛从关注此事跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
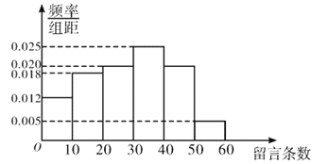
,![]() ,得到如图所示的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如下表:
,得到如图所示的频率分布直方图;并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如下表:
一般关注 | 强烈关注 | 合计 | |
男 | 60 | ||
女 | 5 | 40 | |
合计 | 100 |
(1)补全列联表中数据,并判断能否有![]() 的把握认为网友对此事件是否为“强烈关注”与性别有关?
的把握认为网友对此事件是否为“强烈关注”与性别有关?
(2)现已从男性网友中分层抽样选取了6人,再从这6人中随机选取2人,求这2人中至少有1人属于“强烈关注”的概率.
附: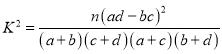 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某乡镇为了发展旅游行业,决定加强宣传,据统计,广告支出费![]() 与旅游收入
与旅游收入![]() (单位:万元)之间有如下表对应数据:
(单位:万元)之间有如下表对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求旅游收入![]() 对广告支出费
对广告支出费![]() 的线性回归方程
的线性回归方程![]() ,若广告支出费
,若广告支出费![]() 万元,预测旅游收入;
万元,预测旅游收入;
(2)在已有的五组数据中任意抽取两组,根据(1)中的线性回归方程,求至少有一组数据,其预测值与实际值之差的绝对值不超过![]() 的概率.(参考公式:
的概率.(参考公式: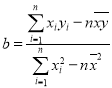 ,
,![]() ,其中
,其中![]() 为样本平均值,参考数据:
为样本平均值,参考数据:![]() ,
,![]() ,
,![]() )
)
【题目】为了调查某大学学生在周日上网的时间,随机对![]() 名男生和
名男生和![]() 名女生进行了不记名的问卷调查,得到了如下的统计结果:
名女生进行了不记名的问卷调查,得到了如下的统计结果:
表1:男生上网时间与频数分布表:
上网时间(分钟) |
|
|
|
|
|
人数 | 5 | 25 | 30 | 25 | 15 |
表2:女生上网时间与频数分布表:
上网时间(分钟) |
|
|
|
|
|
人数 | 10 | 20 | 40 | 20 | 10 |
(1)若该大学共有女生![]() 人,试估计其中上网时间不少于
人,试估计其中上网时间不少于![]() 分钟的人数;
分钟的人数;
(2)完成表3的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“学生周日上网时间与性别有关”?
的把握认为“学生周日上网时间与性别有关”?
(3)从表3的男生中“上网时间少于![]() 分钟”和“上网时间不少于
分钟”和“上网时间不少于![]() 分钟”的人数中用分层抽样的方法抽取一个容量为
分钟”的人数中用分层抽样的方法抽取一个容量为![]() 的样本,再从中任取两人,求至少有一人上网时间超过
的样本,再从中任取两人,求至少有一人上网时间超过![]() 分钟的概率.表3:
分钟的概率.表3:
上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: ,其中
,其中![]() ,
,
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |