题目内容
(本题20分,第1小题满分4分,第2小题满分6分,第3小题6分,第4小题4分)
我们知道,判断直线与圆的位置关系可以用圆心到直线的距离进行判别,那么直线与椭圆的位置关系有类似的判别方法吗?请同学们进行研究并完成下面问题。
(1)设F1、F2是椭圆 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线 的距离分别为d1、d2,试求d1·d2的值,并判断直线L与椭圆M的位置关系。
的距离分别为d1、d2,试求d1·d2的值,并判断直线L与椭圆M的位置关系。
(2)设F1、F2是椭圆 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线  (m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1·d2的值。
(m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1·d2的值。
(3)试写出一个能判断直线与椭圆的位置关系的充要条件,并证明。
(4)将(3)中得出的结论类比到其它曲线,请同学们给出自己研究的有关结论(不必证明)。
我们知道,判断直线与圆的位置关系可以用圆心到直线的距离进行判别,那么直线与椭圆的位置关系有类似的判别方法吗?请同学们进行研究并完成下面问题。
(1)设F1、F2是椭圆
 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线 的距离分别为d1、d2,试求d1·d2的值,并判断直线L与椭圆M的位置关系。
的距离分别为d1、d2,试求d1·d2的值,并判断直线L与椭圆M的位置关系。(2)设F1、F2是椭圆
 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线  (m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1·d2的值。
(m、n不同时为0)的距离分别为d1、d2,且直线L与椭圆M相切,试求d1·d2的值。(3)试写出一个能判断直线与椭圆的位置关系的充要条件,并证明。
(4)将(3)中得出的结论类比到其它曲线,请同学们给出自己研究的有关结论(不必证明)。
(本题20分,第1小题满分4分,第2小题满分6分,第3小题6分,第4小题4分)
(1) ; ………………2分
; ………………2分
联立方程 ; …………3分
; …………3分
 与椭圆M相交。 …………4分
与椭圆M相交。 …………4分
(2)联立方程组
消去

(3)设F1、F2是椭圆 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线
 的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为:
的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为: ;直线L与椭圆M相切的充要条件为:
;直线L与椭圆M相切的充要条件为: ;直线L与椭圆M相离的充要条件为:
;直线L与椭圆M相离的充要条件为: ……14分
……14分
证明:由(2)得,直线L与椭圆M相交

命题得证。
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
(4)可以类比到双曲线:设F1、F2是双曲线 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线 距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为:
距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为: ;直线L与双曲线M相切的充要条件为:
;直线L与双曲线M相切的充要条件为: ;直线L与双曲线M相离的充要条件为:
;直线L与双曲线M相离的充要条件为: ………………20分
………………20分
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
(1)
 ; ………………2分
; ………………2分联立方程
 ; …………3分
; …………3分 与椭圆M相交。 …………4分
与椭圆M相交。 …………4分(2)联立方程组

消去

(3)设F1、F2是椭圆
 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线 的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为:
的距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与椭圆相交的充要条件为: ;直线L与椭圆M相切的充要条件为:
;直线L与椭圆M相切的充要条件为: ;直线L与椭圆M相离的充要条件为:
;直线L与椭圆M相离的充要条件为: ……14分
……14分证明:由(2)得,直线L与椭圆M相交


命题得证。
(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
(4)可以类比到双曲线:设F1、F2是双曲线
 的两个焦点,点F1、F2到直线
的两个焦点,点F1、F2到直线 距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为:
距离分别为d1、d2,且F1、F2在直线L的同侧。那么直线L与双曲线相交的充要条件为: ;直线L与双曲线M相切的充要条件为:
;直线L与双曲线M相切的充要条件为: ;直线L与双曲线M相离的充要条件为:
;直线L与双曲线M相离的充要条件为: ………………20分
………………20分(写出其他的充要条件仅得2分,未指出“F1、F2在直线L的同侧”得3分)
同答案

练习册系列答案
相关题目
 (
( )的长轴,若把AB100等分,过每个分点作AB的垂线,交椭圆的上半部分于P1、P2、…、P99 ,F1为椭圆的左焦点,则
)的长轴,若把AB100等分,过每个分点作AB的垂线,交椭圆的上半部分于P1、P2、…、P99 ,F1为椭圆的左焦点,则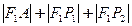 +…
+… 的值是 ( )
的值是 ( )



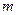 的取值范围,使得椭圆
的取值范围,使得椭圆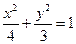 上有不同两点关于直线
上有不同两点关于直线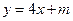 对称.
对称.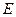 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过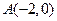 、
、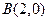 、
、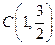 三点.
三点.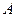 、
、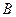 的任意一点,
的任意一点,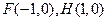 ,当
,当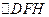 内切圆的面积最大时。求内切圆圆心的坐标;
内切圆的面积最大时。求内切圆圆心的坐标;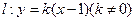 与椭圆
与椭圆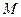 、
、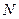 两点,证明直线
两点,证明直线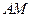 与直线
与直线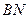 的交点在直线
的交点在直线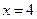 上.
上.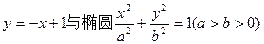 相交于
相交于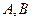 两点,且
两点,且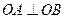 (其中O为坐标原点).
(其中O为坐标原点).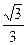 ,求椭圆的标准方程;(2)求证:不论
,求椭圆的标准方程;(2)求证:不论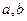 如何变化,椭圆恒过第一象限内的一个定点
如何变化,椭圆恒过第一象限内的一个定点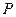 ,并求点
,并求点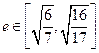 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.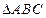 的周长为16,且
的周长为16,且 ,则顶点
,则顶点 的轨迹是( )
的轨迹是( ) 是椭圆
是椭圆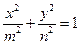 (
( ,
, )上两点,且
)上两点,且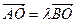 ,则
,则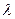 =
=  ,则
,则 与
与 的大小关系为__________________。
的大小关系为__________________。