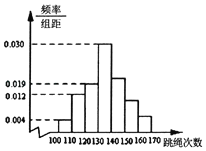
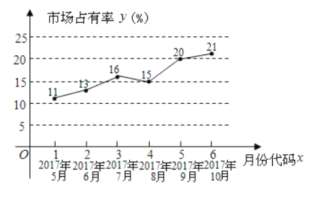
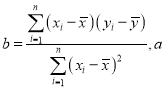��Ŀ����
����Ŀ������С������12�֣�������С��6�֣�������С��6�֣�һ�ҹ�˾�ƻ�����ij��С�Ͳ�Ʒ���¹̶��ɱ�Ϊ![]() ��Ԫ��ÿ����
��Ԫ��ÿ����![]() �����Ҫ��Ͷ��
�����Ҫ��Ͷ��![]() ��Ԫ.��ù�˾һ������������С�Ͳ�Ʒ
��Ԫ.��ù�˾һ������������С�Ͳ�Ʒ![]() �����ȫ�������꣬ÿ�������������Ϊ
�����ȫ�������꣬ÿ�������������Ϊ![]() ��Ԫ����ÿ������Ҹ��貹��
��Ԫ����ÿ������Ҹ��貹��![]() ��Ԫ. ��
��Ԫ. ��![]() Ϊ��Ȼ�����ĵ�����
Ϊ��Ȼ�����ĵ�����![]() ��һ������.��
��һ������.��
������д��������![]() ����Ԫ�������²���
����Ԫ�������²���![]() ��������ĺ�������ʽ��
��������ĺ�������ʽ��
������������������![]() ���ʱ����ù�˾����������С�Ͳ�Ʒ������õ����������ֵ����Ԫ������ʱ����������ֵ�������. ��ע��������=����������+�¹��Ҳ���-���ܳɱ���.
���ʱ����ù�˾����������С�Ͳ�Ʒ������õ����������ֵ����Ԫ������ʱ����������ֵ�������. ��ע��������=����������+�¹��Ҳ���-���ܳɱ���.
���𰸡�������![]() ��
��
����������������![]() ���ʱ���ù�˾����������С�Ͳ�Ʒ������õ����������ֵΪ
���ʱ���ù�˾����������С�Ͳ�Ʒ������õ����������ֵΪ![]() ����ʱ����������ֵΪ
����ʱ����������ֵΪ![]() �������
�������
��������
���⣨������������������������=����������+�¹��Ҳ���-���ܳɱ����ɵ�����![]() ����Ԫ�������²���
����Ԫ�������²���![]() ��������ĺ�������ʽ
��������ĺ�������ʽ![]() ��
��
������������![]() �ĵ����������õ���
�ĵ����������õ���![]() �ķ����жϺ�����
�ķ����жϺ�����![]() �ĵ����Բ���һ���ݴ���������ֵ�����ֵ��.
�ĵ����Բ���һ���ݴ���������ֵ�����ֵ��.
����������⣺���������ڣ�������=����������+�¹��Ҳ���-���ܳɱ����ɵ�
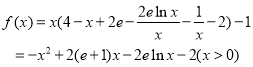
������![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() ��
��
��![]()
�б����£�
|
|
|
|
| + |
| - |
| �� | ����ֵ | �� |
���ϱ��ã�![]() �ڶ�����
�ڶ�����![]() �ϵ����ֵΪ
�ϵ����ֵΪ![]() .
.
��![]() .��������������
.��������������![]() ���ʱ���ù�˾����������С�Ͳ�Ʒ������õ����������ֵΪ
���ʱ���ù�˾����������С�Ͳ�Ʒ������õ����������ֵΪ![]() ����ʱ����������ֵΪ
����ʱ����������ֵΪ![]() �������.
�������.

����Ŀ����2018��2019ÿ�߿���ѧȫ������У���22�⿼������ϵ�Ͳ������̣���23�⿼�鲻��ʽѡ��.2018���{��������ijУ��ͳ�Ʒ���:ѡ���22��Ŀ����϶ಢ�ҵ÷���Ҳ�ϸ�.Ϊ�о�2019��ѡ����÷��������У������������������ȫ����2019��߿�ѡ����ģʽ���ڲ��Խ�����У��ѧ��ʦ��ȫУ����ѧ����ѡ����÷ֽ��г���ͳ�ƣ��õ�����÷ֵ�ͳ�Ʊ�����(��֪ÿ��ѧ��ֻѡ��������):
��22��ĵ÷�ͳ�Ʊ�
�÷� | 0 | 3 | 5 | 8 | 10 |
�������� | 50 | 50 | 75 | 125 | 200 |
�Ŀ����� | 25 | 25 | 125 | 0 | 25 |
��23��ĵ÷�ͳ�Ʊ�
�÷� | 0 | 3 | 5 | 8 | 10 |
�������� | 30 | 52 | 58 | 60 | 200 |
�Ŀ����� | 5 | 10 | 10 | 5 | 70 |
(1)�������2��2�����������ж��ܷ���99%�İ�����Ϊ��ѡ�����ѡ���롰�ġ����ƵĿ��ࡱ�йأ�
ѡ��22�� | ѡ��23�� | �ܼ� | |
�������� | |||
�Ŀ����� | |||
�ܼ� |
(2)����ȫ�����ѧ��ѡ���ƽ���÷���Ϊ�������ݣ�������ǿ�������������ͳ�����ݣ����ѡ���ĵ��⣬��˵������.
��:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |