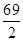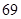题目内容
已知数列{an}的首项a1=2,?n∈N*,点(an,an+1)都在直线x-2y+1=0上.
(1)证明:数列{an-1}是等比数列;
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn.
(1)证明:数列{an-1}是等比数列;
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn.
(1)证明:∵点(an,an+1)都在直线x-2y+1=0上,∴an-2an+1+1=0,
变形为an-1=2(an+1-1),an+1-1=
(an-1),又a1-1=1≠0,
∴数列{an-1}是等比数列,首项为1,公比为
.
(2)由(1)得an-1=1×(
)n-1,
∴an=1+21-n.
(3)Sn=(1+20)+(1+2-1)+(1+2-2)+…+(1+21-n)
=n+(20+2-1+2-2+…+21-n)
=n+
=n+2-21-n.
变形为an-1=2(an+1-1),an+1-1=
| 1 |
| 2 |
∴数列{an-1}是等比数列,首项为1,公比为
| 1 |
| 2 |
(2)由(1)得an-1=1×(
| 1 |
| 2 |
∴an=1+21-n.
(3)Sn=(1+20)+(1+2-1)+(1+2-2)+…+(1+21-n)
=n+(20+2-1+2-2+…+21-n)
=n+
| 1-2-n |
| 1-2-1 |
=n+2-21-n.

练习册系列答案
相关题目
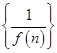 (n∈N*)的前n项和是( )
(n∈N*)的前n项和是( )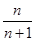
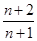
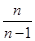
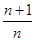
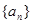 的前
的前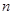 项和为
项和为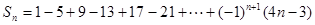 ,则
,则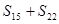 的值是( )
的值是( )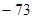
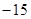
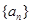 是由正数组成的等比数列,
是由正数组成的等比数列,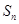 表示
表示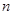 项的和,若
项的和,若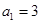 ,
,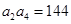 ,则
,则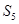 的值是 ( )
的值是 ( )