题目内容
已知下列数列{an}的前n项和Sn,求{an}的通项公式:
(1)Sn=2n2-3n;
(2)Sn=3n+b.
(1)Sn=2n2-3n;
(2)Sn=3n+b.
(1)∵Sn=2n2-3n,
∴当n=1时,a1=S1=2-3=-1,
当n≥2时,an=Sn-Sn-1
=(2n2-3n)-[2(n-1)2-3(n-1)]=4n-5,
由于a1也适合此等式,
∴an=4n-5.
(2)∵Sn=3n+b,
∴当n=1时,a1=S1=3+b,
当n≥2时,an=Sn-Sn-1
=(3n+b)-(3n-1+b)=2•3n-1.
当b=-1时,a1适合此等式;
当b≠-1时,a1不适合此等式.
∴当b=-1时,an=2•3n-1;
当b≠-1时,an=
.
∴当n=1时,a1=S1=2-3=-1,
当n≥2时,an=Sn-Sn-1
=(2n2-3n)-[2(n-1)2-3(n-1)]=4n-5,
由于a1也适合此等式,
∴an=4n-5.
(2)∵Sn=3n+b,
∴当n=1时,a1=S1=3+b,
当n≥2时,an=Sn-Sn-1
=(3n+b)-(3n-1+b)=2•3n-1.
当b=-1时,a1适合此等式;
当b≠-1时,a1不适合此等式.
∴当b=-1时,an=2•3n-1;
当b≠-1时,an=
|

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
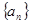 的通项公式
的通项公式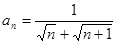 ,则该数列的前_________项之和等于
,则该数列的前_________项之和等于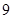 .
.