题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 均在第一象限),
均在第一象限),![]() 为坐标原点.
为坐标原点.
①证明:直线![]() 的斜率依次成等比数列.
的斜率依次成等比数列.
②若![]() 与
与![]() 关于
关于![]() 轴对称,证明:
轴对称,证明:![]() .
.
【答案】(1)![]() ; (2)①见解析;②见解析.
; (2)①见解析;②见解析.
【解析】
(1)根据离心率、焦距和![]() 可解出
可解出![]() ,从而得到椭圆方程;(2)①设直线
,从而得到椭圆方程;(2)①设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() ,将直线方程与椭圆方程联立可得韦达定理的形式,从而求得
,将直线方程与椭圆方程联立可得韦达定理的形式,从而求得![]() ;整理可知:
;整理可知:![]() ,从而证得结论;②
,从而证得结论;②![]() 与
与![]() 关于
关于![]() 轴对称可知
轴对称可知![]() ,由①知
,由①知![]() ,则
,则![]() ,利用两角和差正切公式展开整理,根据基本不等式求得最小值,经验证等号无法取得,从而证得结论.
,利用两角和差正切公式展开整理,根据基本不等式求得最小值,经验证等号无法取得,从而证得结论.
(1)由题意可得: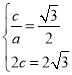 ,解得:
,解得:
![]()
![]() 椭圆
椭圆![]() 的方程为:
的方程为:![]()
(2)证明:①设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]()
由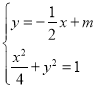 消去
消去![]() 得:
得:![]()
则![]() ,且
,且![]() ,
,![]()
![]()
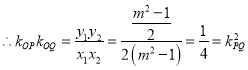
即直线![]() 的斜率依次成等比数列
的斜率依次成等比数列
②由题可知:![]()
由①可知:![]() ,
,![]() ,
,![]()
![]()
![]()
若![]() ,则
,则![]() 两点重合,不符合题意;可知无法取得等号
两点重合,不符合题意;可知无法取得等号
![]()

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如表的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
算得,![]() .见附表:参照附表,得到的正确结论是( )
.见附表:参照附表,得到的正确结论是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C. 有99%以上的把握认为“爱好该项运动与性别有关”
D. 有99%以上的把握认为“爱好该项运动与性别无关”
【题目】某企业购买某种仪器,在仪器使用期间可能出现故障,需要请销售仪器的企业派工程师进行维修,因为考虑到人力、成本等多方面的原因,销售仪器的企业提供以下购买仪器维修服务的条件:在购买仪器时,可以直接购买仪器维修服务,维修一次1000元;在仪器使用期间,如果维修服务次数不够再次购买,则需要每次1500元..现需决策在购买仪器的同时购买几次仪器维修服务,为此搜集并整理了500台这种机器在使用期内需要维修的次数,得到如下表格:
维修次数 | 5 | 6 | 7 | 8 | 9 |
频数(台) | 50 | 100 | 150 | 100 | 100 |
记![]() 表示一台仪器使用期内维修的次数,
表示一台仪器使用期内维修的次数,![]() 表示一台仪器使用期内维修所需要的费用,
表示一台仪器使用期内维修所需要的费用,![]() 表示购买仪器的同时购买的维修服务的次数.
表示购买仪器的同时购买的维修服务的次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)以这500台仪器使用期内维修次数的频率代替一台仪器维修次数发生的概率,求![]() 的概率.
的概率.
(3)假设购买这500台仪器的同时每台都购买7次维修服务,或每台都购买8次维修服务,请分别计算这500台仪器在购买维修服务所需要费用的平均数,以此为决策依据,判断购买7次还是8次维修服务?