题目内容
7.已知函数f(x)的值域为[$\frac{3}{8},\frac{4}{9}$],求g(x)=f(x)+$\sqrt{1-2f(x)}$的最值.分析 通过换元得到g(t)=t+$\sqrt{1-2t}$.又设$\sqrt{1-2t}$=k,求出k的范围,得到g(k)=-$\frac{{(k-1)}^{2}-2}{2}$,根据二次函数的性质,求出函数的值域即可.
解答 解:设f(x)=t,则$\frac{3}{8}$≤t≤$\frac{4}{9}$.
∴g(t)=t+$\sqrt{1-2t}$.
又设$\sqrt{1-2t}$=k,故有t=$\frac{1{-k}^{2}}{2}$.
则$\frac{1}{3}$≤k≤$\frac{1}{2}$.(可由t的范围求得)
故g(k)=$\frac{1{-k}^{2}}{2}$+k=-$\frac{{(k-1)}^{2}-2}{2}$.
∵$\frac{1}{3}$≤k≤$\frac{1}{2}$,
∴当k=$\frac{1}{3}$时,有最小值$\frac{7}{9}$
当k=$\frac{1}{2}$时,有最大值$\frac{7}{8}$,
∴值域[$\frac{7}{9}$,$\frac{7}{8}$].
点评 本题考查了二次函数的值域问题,考查换元思想,求出k的范围,得到g(k)=-$\frac{{(k-1)}^{2}-2}{2}$是解题的关键,本题是一道中档题.

练习册系列答案
相关题目
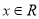 ,则“
,则“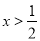 ”是“
”是“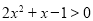 ”的( )
”的( )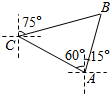 如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.
如图所示,一艘海轮从A处出发,测得灯塔在海轮的北偏东15°方向,与海轮相距20海里的B处,海轮按北偏西60°的方向航行了30分钟后到达C处,又测得灯塔在海轮的北偏东75°的方向,则海轮的速度为$\frac{2}{3}$($\sqrt{3}$-1)海里/分钟.