题目内容
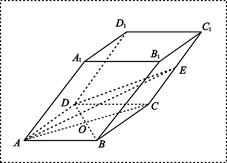
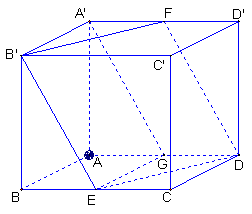
(满分14分)在斜四棱柱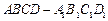 中,已知底面
中,已知底面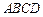 是边长为4的菱形,
是边长为4的菱形,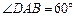 ,且点
,且点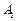 在面
在面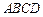 上的射影是底面对角线
上的射影是底面对角线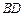 与AC的交点O,设点E是
与AC的交点O,设点E是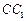 的中点,
的中点,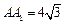 .
.
(Ⅰ) 求证:四边形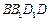 是矩形;
是矩形;
(Ⅱ) 求二面角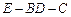 的大小;
的大小;
 (Ⅲ) 求四面体
(Ⅲ) 求四面体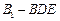 的体积.
的体积.
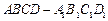 中,已知底面
中,已知底面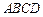 是边长为4的菱形,
是边长为4的菱形,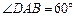 ,且点
,且点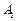 在面
在面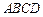 上的射影是底面对角线
上的射影是底面对角线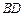 与AC的交点O,设点E是
与AC的交点O,设点E是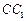 的中点,
的中点,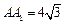 .
.(Ⅰ) 求证:四边形
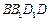 是矩形;
是矩形;(Ⅱ) 求二面角
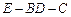 的大小;
的大小; (Ⅲ) 求四面体
(Ⅲ) 求四面体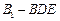 的体积.
的体积.(I)略 (Ⅱ)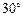 (Ⅲ)
(Ⅲ)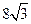

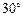 (Ⅲ)
(Ⅲ)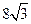

解法一:(Ⅰ) 连接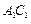 .
.
因为四边形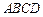 为菱形,
为菱形,
所以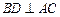 ,又
,又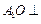 面
面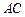 ,[所以
,[所以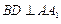 .
.
而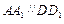 ,所以
,所以 .因为四边形
.因为四边形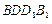 是平行四边形,所以四边形
是平行四边形,所以四边形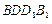 是矩形.
是矩形.
(Ⅱ) 连接OE,因为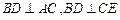 ,所以
,所以 平面
平面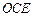 ,∴
,∴ 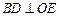 ,即
,即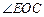 为二面角
为二面角
E─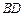 ─C的平面角.在菱形
─C的平面角.在菱形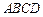 中,
中,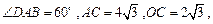
又E是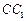 的中点,
的中点,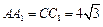 .所以
.所以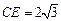 .
.
在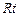 △
△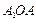 中,
中,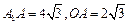 ,∴
,∴ 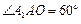 ,
,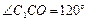 ,
,
所以在△ 中,有
中,有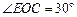 ,即二面角E─BD─C的大小为
,即二面角E─BD─C的大小为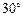 . 9分
. 9分
(Ⅲ) 设点D到平面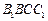 的距离为h,则有
的距离为h,则有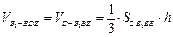 .
.
因为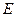 是
是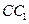 的中点,所以
的中点,所以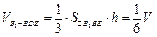
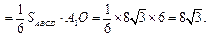 14分
14分
解法二:(Ⅰ) 连结AC、BD相交于O,连结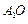 .
.
由已知,有AC⊥BD,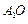 ⊥面ABCD,故可建立空间直角坐标系
⊥面ABCD,故可建立空间直角坐标系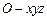 ,
,
且以下各点的坐标分别为: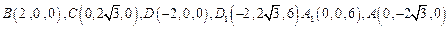 , 1分
, 1分
设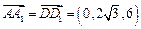 ,
, 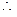
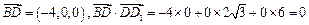 ,
,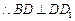 3分又
3分又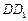
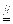
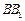 ,
, 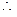 四边形
四边形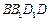 为平行四边形.
为平行四边形.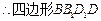 是矩形. 4分
是矩形. 4分
(Ⅱ) 设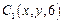 ,则
,则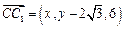 .
.
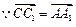 , 由
, 由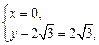 可求得
可求得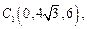
∴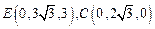 .设
.设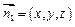 为平面EBD的法向量,
为平面EBD的法向量,
则由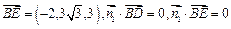 ,得
,得
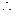 可取
可取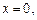
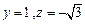 ,
,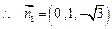 . 6分
. 6分
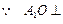 平面
平面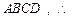 平面BDC的法向量为
平面BDC的法向量为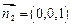
 ,
,
而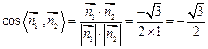 .
.
∴ 二面角E─BD─C的大小为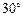 . 9分
. 9分
(Ⅲ) 设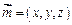 为平面
为平面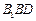 的法向量,
的法向量,
则由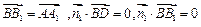 ,得
,得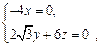
∴ 可取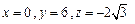 ,
,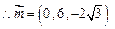 .
.
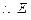 到平面
到平面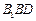 的距离
的距离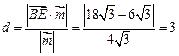 . 11分
. 11分
而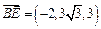 ,又由(Ⅰ)知,
,又由(Ⅰ)知,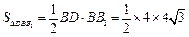 ,
,
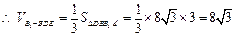 .················ 14分
.················ 14分
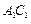 .
. 因为四边形
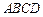 为菱形,
为菱形,所以
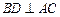 ,又
,又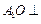 面
面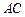 ,[所以
,[所以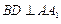 .
. 而
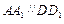 ,所以
,所以 .因为四边形
.因为四边形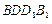 是平行四边形,所以四边形
是平行四边形,所以四边形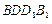 是矩形.
是矩形.(Ⅱ) 连接OE,因为
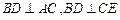 ,所以
,所以 平面
平面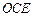 ,∴
,∴ 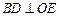 ,即
,即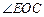 为二面角
为二面角E─
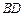 ─C的平面角.在菱形
─C的平面角.在菱形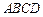 中,
中,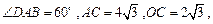
又E是
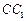 的中点,
的中点,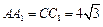 .所以
.所以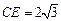 .
.在
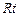 △
△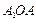 中,
中,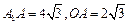 ,∴
,∴ 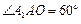 ,
,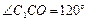 ,
,所以在△
 中,有
中,有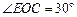 ,即二面角E─BD─C的大小为
,即二面角E─BD─C的大小为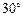 . 9分
. 9分(Ⅲ) 设点D到平面
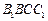 的距离为h,则有
的距离为h,则有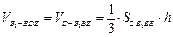 .
.因为
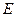 是
是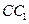 的中点,所以
的中点,所以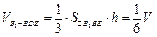
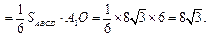 14分
14分解法二:(Ⅰ) 连结AC、BD相交于O,连结
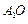 .
.由已知,有AC⊥BD,
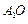 ⊥面ABCD,故可建立空间直角坐标系
⊥面ABCD,故可建立空间直角坐标系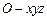 ,
,且以下各点的坐标分别为:
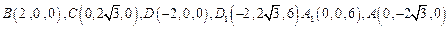 , 1分
, 1分设
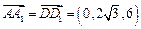 ,
, 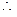
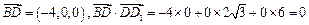 ,
,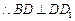 3分又
3分又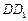
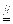
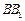 ,
, 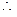 四边形
四边形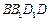 为平行四边形.
为平行四边形.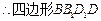 是矩形. 4分
是矩形. 4分(Ⅱ) 设
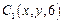 ,则
,则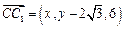 .
.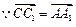 , 由
, 由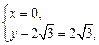 可求得
可求得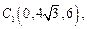
∴
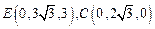 .设
.设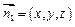 为平面EBD的法向量,
为平面EBD的法向量,则由
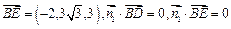 ,得
,得
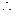 可取
可取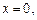
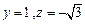 ,
,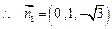 . 6分
. 6分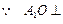 平面
平面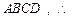 平面BDC的法向量为
平面BDC的法向量为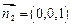
 ,
,而
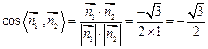 .
. ∴ 二面角E─BD─C的大小为
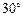 . 9分
. 9分(Ⅲ) 设
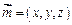 为平面
为平面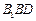 的法向量,
的法向量,则由
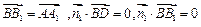 ,得
,得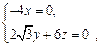
∴ 可取
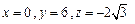 ,
,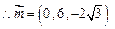 .
. 到平面
到平面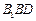 的距离
的距离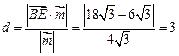 . 11分
. 11分 而
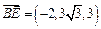 ,又由(Ⅰ)知,
,又由(Ⅰ)知,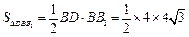 ,
,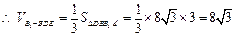 .················ 14分
.················ 14分
练习册系列答案
相关题目
 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为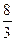 .
.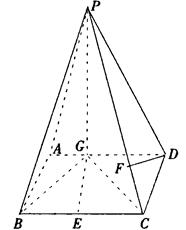 (Ⅱ)求点D到平面PBG的距离;
(Ⅱ)求点D到平面PBG的距离;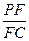 的值.
的值.
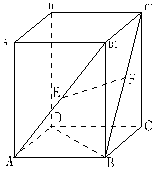
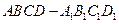 中,E、F
中,E、F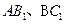 的中点,则以下结论中不成立的是
的中点,则以下结论中不成立的是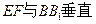
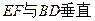
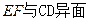
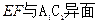
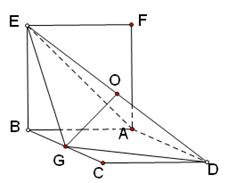 如图,正方形
如图,正方形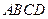 和
和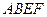 的边长均为1,且它们所在平面互相垂直,
的边长均为1,且它们所在平面互相垂直,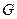 为线段
为线段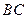 的中点,
的中点, 为线段
为线段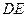 的中点。
的中点。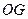 ∥面
∥面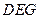 ⊥平面
⊥平面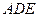 ;
;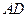 与平面
与平面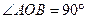 ,
,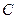 为空间中一点,且
为空间中一点,且 ,则直线
,则直线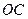 与平面
与平面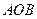 所成角
所成角 的正弦值为
的正弦值为 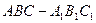 的所有棱长均为
的所有棱长均为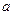 ,侧面
,侧面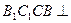 底面
底面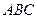 ,且
,且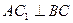 .
.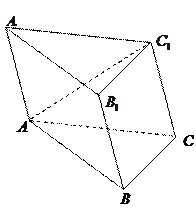
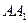 与
与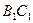 间的距离;
间的距离;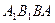 与底面
与底面 ,点P是棱DD1的中点,
,点P是棱DD1的中点, ,AB=1,若点Q在侧面
,AB=1,若点Q在侧面 (包括其边界)上运动,且总保持
(包括其边界)上运动,且总保持 ,则动点Q的轨迹是 ( )
,则动点Q的轨迹是 ( )