题目内容
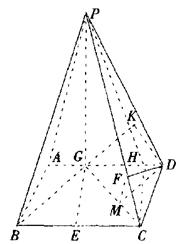
已知,如图四棱锥P—ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG= GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为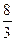 .
.
(Ⅰ)求异面直线GE与PC所成的角;
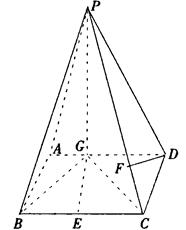 (Ⅱ)求点D到平面PBG的距离;
(Ⅱ)求点D到平面PBG的距离;
(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求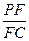 的值.
的值.
 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为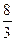 .
.(Ⅰ)求异面直线GE与PC所成的角;
 (Ⅱ)求点D到平面PBG的距离;
(Ⅱ)求点D到平面PBG的距离;(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求
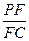 的值.
的值.见解析
解法一: (I)由已知
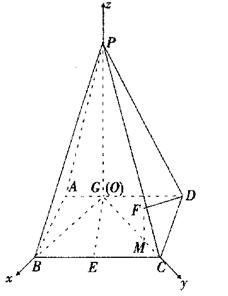
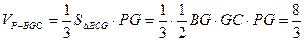
∴PG=4
如图所示,以G点为原点建立空间直角坐标系
o—xyz,则
B(2,0,0),C(0,2,0),P(0,0,4)
故E(1,1,0)
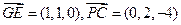
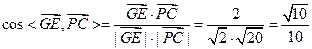 ∴异面直线GE与PC所成的角为arccos
∴异面直线GE与PC所成的角为arccos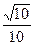
(II)平面PBG的单位法向量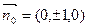
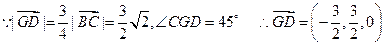
∴点D到平面PBG的距离为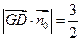
(III)设F(0,y , z)
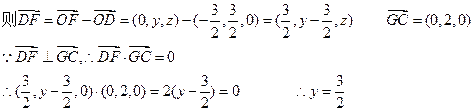
在平面PGC内过F点作FM⊥GC,M为垂足,则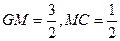
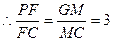
解法二:
 (I)由已知
(I)由已知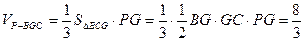
∴PG=4
在平面ABCD内,过C点作CH//EG交AD于H,连结PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角.
在△PCH中,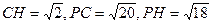
由余弦定理得,cos∠PCH=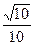 ,∴异面直线GE与PC所成的角为arccos
,∴异面直线GE与PC所成的角为arccos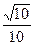
(II)∵PG⊥平面ABCD,PG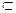 平面PBG ∴平面PBG⊥平面ABCD
平面PBG ∴平面PBG⊥平面ABCD
在平面ABCD内,过D作DK⊥BG,交BG延长线于K,
则DK⊥平面PBG ∴DK的长就是点D到平面PBG的距离
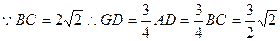
在△DKG,DK=DGsin45°=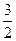 ∴点D到平面PBG的距离为
∴点D到平面PBG的距离为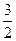
(III)在平面ABCD内,过D作DM⊥GC,M为垂足,连结MF,又因为DF⊥GC
∴GC⊥平面MFD,∴GC⊥FM
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD ∴FM//PG
由GM⊥MD得:GM=GD·cos45°=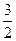
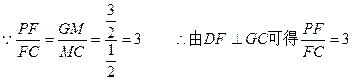

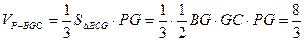
∴PG=4
如图所示,以G点为原点建立空间直角坐标系
o—xyz,则
B(2,0,0),C(0,2,0),P(0,0,4)
故E(1,1,0)
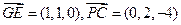
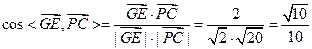 ∴异面直线GE与PC所成的角为arccos
∴异面直线GE与PC所成的角为arccos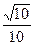
(II)平面PBG的单位法向量
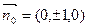
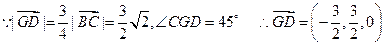
∴点D到平面PBG的距离为
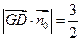
(III)设F(0,y , z)
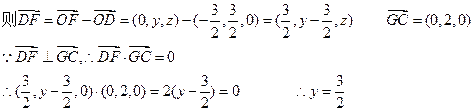
在平面PGC内过F点作FM⊥GC,M为垂足,则
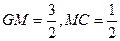
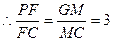
解法二:
 (I)由已知
(I)由已知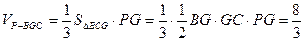
∴PG=4
在平面ABCD内,过C点作CH//EG交AD于H,连结PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角.
在△PCH中,
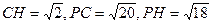
由余弦定理得,cos∠PCH=
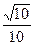 ,∴异面直线GE与PC所成的角为arccos
,∴异面直线GE与PC所成的角为arccos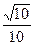
(II)∵PG⊥平面ABCD,PG
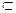 平面PBG ∴平面PBG⊥平面ABCD
平面PBG ∴平面PBG⊥平面ABCD在平面ABCD内,过D作DK⊥BG,交BG延长线于K,
则DK⊥平面PBG ∴DK的长就是点D到平面PBG的距离
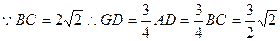
在△DKG,DK=DGsin45°=
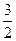 ∴点D到平面PBG的距离为
∴点D到平面PBG的距离为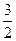
(III)在平面ABCD内,过D作DM⊥GC,M为垂足,连结MF,又因为DF⊥GC
∴GC⊥平面MFD,∴GC⊥FM
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD ∴FM//PG
由GM⊥MD得:GM=GD·cos45°=
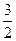

练习册系列答案
相关题目
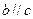 ,且直线
,且直线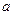 与
与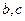 都相交,求证:直线
都相交,求证:直线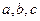 共面。
共面。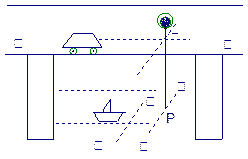
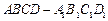 中,已知底面
中,已知底面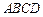 是边长为4的菱形,
是边长为4的菱形,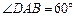 ,且点
,且点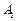 在面
在面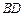 与AC的交点O,设点E是
与AC的交点O,设点E是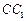 的中点,
的中点,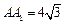 .
.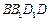 是矩形;
是矩形;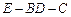 的大小;
的大小;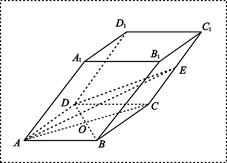 (Ⅲ) 求四面体
(Ⅲ) 求四面体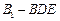 的体积.
的体积. 的平面去截球,所得的截面面积为
的平面去截球,所得的截面面积为 ,则球的体积为( )
,则球的体积为( )



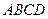 中,
中,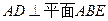 ,
,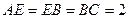 ,
,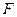 为
为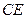 上的点,且
上的点,且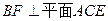 .
.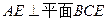 ;(Ⅱ)求证;
;(Ⅱ)求证;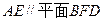 ;
;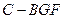 的体积.
的体积.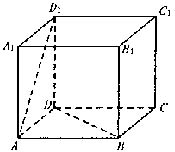 如图,正方体ABCD—A1B1C1D1的棱长为1,PQ分别是线段AD1和BD上的点,且D1P∶PA=DQ∶QB=5∶12.
如图,正方体ABCD—A1B1C1D1的棱长为1,PQ分别是线段AD1和BD上的点,且D1P∶PA=DQ∶QB=5∶12. 上的函数
上的函数 ,其中
,其中 为常数.
为常数. ,求证:函数
,求证:函数 在区间
在区间 上是增函数;
上是增函数; ,在
,在 处取得最大值,求正数
处取得最大值,求正数