题目内容
α、β是两个不同的平面,m,n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n,②α⊥β,③n⊥β,④m⊥α.以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题,并证明它.
m⊥α,n⊥β,α⊥β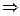 m⊥n(或m⊥n,m⊥α,n⊥β
m⊥n(或m⊥n,m⊥α,n⊥β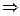 α⊥β)
α⊥β)
证明如下:过不在α、β内的任一点P,作PM∥m,PN∥n
过PM、PN作平面r交α于MQ,交β于NQ.

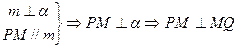 ,
,
同理PN⊥NQ.
因此∠MPN+∠MQN = 180°,
故∠MQN = 90°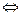 ∠MPN = 90°
∠MPN = 90°
即α⊥β m⊥n.
m⊥n.
 m⊥n(或m⊥n,m⊥α,n⊥β
m⊥n(或m⊥n,m⊥α,n⊥β α⊥β)
α⊥β)证明如下:过不在α、β内的任一点P,作PM∥m,PN∥n
过PM、PN作平面r交α于MQ,交β于NQ.

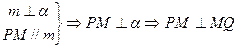 ,
,同理PN⊥NQ.
因此∠MPN+∠MQN = 180°,
故∠MQN = 90°
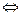 ∠MPN = 90°
∠MPN = 90°即α⊥β
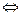 m⊥n.
m⊥n.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图所示,四棱锥
如图所示,四棱锥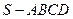 的底面是边长为1的正方形,
的底面是边长为1的正方形,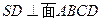 ,
,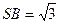 ,
,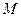 点是棱
点是棱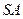 的中点。
的中点。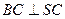 ;
;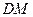 与
与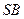 所成的角的大小;
所成的角的大小;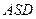 与面
与面 所成二面角的大小。
所成二面角的大小。 ,且直线
,且直线 与
与 都相交,求证:直线
都相交,求证:直线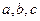 共面。
共面。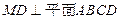 ,
,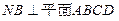 ,且MD=NB=1,E为BC的中点
,且MD=NB=1,E为BC的中点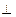 平面AMN?若存在,求线段AS的长;若不存在,请说明理由
平面AMN?若存在,求线段AS的长;若不存在,请说明理由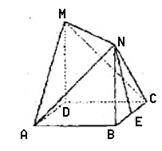


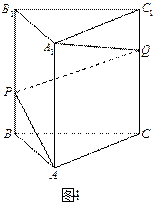 如图4,正三棱柱
如图4,正三棱柱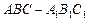 中,
中,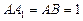 ,
,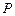 、
、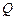 分别是侧棱
分别是侧棱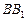 、
、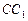 上的点,且使得折线
上的点,且使得折线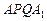 的长
的长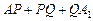 最短.
最短.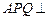 平面
平面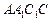 ;(2)求直线
;(2)求直线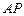 与平面
与平面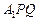 所成角的余弦值.
所成角的余弦值.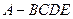 中,
中,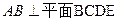 ,
,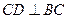 ,
, 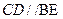 ,
,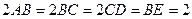 .⑴求证
.⑴求证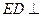 平面
平面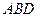 ;
;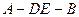 的大小.
的大小.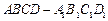 中,已知底面
中,已知底面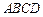 是边长为4的菱形,
是边长为4的菱形,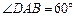 ,且点
,且点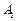 在面
在面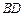 与AC的交点O,设点E是
与AC的交点O,设点E是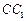 的中点,
的中点,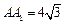 .
.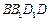 是矩形;
是矩形;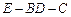 的大小;
的大小;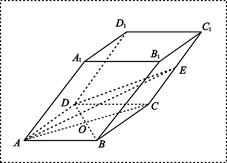 (Ⅲ) 求四面体
(Ⅲ) 求四面体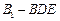 的体积.
的体积.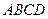 中,
中,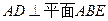 ,
,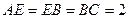 ,
,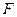 为
为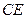 上的点,且
上的点,且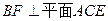 .
.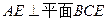 ;(Ⅱ)求证;
;(Ⅱ)求证;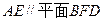 ;
;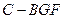 的体积.
的体积. 在同一个球面上,
在同一个球面上,  平面
平面 ,
, ,若
,若 ,
,
 ,
, ,则
,则 两点间的球面距离是 .
两点间的球面距离是 .