ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΈΣΝΥΦλ≤βΡ≥¬÷ΧΞΙΪΥΨ…ζ≤ζΒΡ¬÷ΧΞΒΡΩμΕ»Θ§–η“Σ≥ιΦλ“Μ≈ζ¬÷ΧΞΘ®Ι≤10Ηω¬÷ΧΞΘ©Θ§“―÷Σ’β≈ζ¬÷ΧΞΩμΕ»Θ®ΒΞΈΜΘΚ ![]() Θ©ΒΡ’έœΏΆΦ»γœ¬ΆΦΥυ ΨΘΚ
Θ©ΒΡ’έœΏΆΦ»γœ¬ΆΦΥυ ΨΘΚ

Θ®1Θ©«σ’β≈ζ¬÷ΧΞΩμΕ»ΒΡΤΫΨυ÷ΒΘΜ
Θ®2Θ©œ÷ΫΪ’β≈ζ¬÷ΧΞΥΆ»Ξ÷ Φλ≤ΩΫχ––≥ιΦλΘ§≥ιΦλΖΫΑΗ «ΘΚ¥”’β≈ζ¬÷ΧΞ÷–»Έ»Γ5ΗωΉςΦλ―ιΘ§’β5Ηω¬÷ΧΞΒΡΩμΕ»ΕΦ‘Ύ![]() ΡΎΘ§‘ρ≥Τ’β≈ζ¬÷ΧΞΚœΗώΘ§»γΙϊ≥ιΦλ≤ΜΚœΗώΘ§ΨΆ“Σ÷Ί–¬‘Ό≥ιΦλ“Μ¥ΈΘ§»τΜΙ «≤ΜΚœΗώΘ§’β≈ζ¬÷ΧΞΨΆ»œΕ®≤ΜΚœΗώ.
ΡΎΘ§‘ρ≥Τ’β≈ζ¬÷ΧΞΚœΗώΘ§»γΙϊ≥ιΦλ≤ΜΚœΗώΘ§ΨΆ“Σ÷Ί–¬‘Ό≥ιΦλ“Μ¥ΈΘ§»τΜΙ «≤ΜΚœΗώΘ§’β≈ζ¬÷ΧΞΨΆ»œΕ®≤ΜΚœΗώ.
![]() «σ’β≈ζ¬÷ΧΞΒΎ“Μ¥Έ≥ιΦλΨΆΚœΗώΒΡΗ≈¬ ΘΜ
«σ’β≈ζ¬÷ΧΞΒΎ“Μ¥Έ≥ιΦλΨΆΚœΗώΒΡΗ≈¬ ΘΜ
![]() Φ«
Φ«![]() ΈΣ’β≈ζ¬÷ΧΞΒΡ≥ιΦλ¥Έ ΐΘ§«σ
ΈΣ’β≈ζ¬÷ΧΞΒΡ≥ιΦλ¥Έ ΐΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ.
ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ.
ΓΨ¥πΑΗΓΩΘ®1Θ©195Θ®mmΘ©(2)2![]()
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©”…ΤΫΨυ÷ΒΒΡΕ®“ε«σΤΫΨυ÷ΒΘ§Φ¥![]() ΓΘΘ®2Θ©”…ΤΒ¬ ΙάΦΤΗ≈¬ Θ§’β≈ζ¬÷ΧΞΩμΕ»ΕΦ‘Ύ
ΓΘΘ®2Θ©”…ΤΒ¬ ΙάΦΤΗ≈¬ Θ§’β≈ζ¬÷ΧΞΩμΕ»ΕΦ‘Ύ![]() ΡΎΒΡΗω ΐΈΣ6Θ§Ήή ΐΈΣ10Θ§”…Ι≈ΒδΗ≈–ΆΩ…ΒΟ
ΡΎΒΡΗω ΐΈΣ6Θ§Ήή ΐΈΣ10Θ§”…Ι≈ΒδΗ≈–ΆΩ…ΒΟ![]() ΓΘ”…Χβ“βΩ…÷Σ
ΓΘ”…Χβ“βΩ…÷Σ![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ1,2Θ§
ΒΡΩ…Ρή»Γ÷ΒΈΣ1,2Θ§ ![]() Θ§”…
Θ§”…![]() +
+ ![]() =1Θ§Ω…Υψ≥ω
=1Θ§Ω…Υψ≥ω![]() Θ§–¥≥ωΖ÷≤ΦΝ–ΓΘ
Θ§–¥≥ωΖ÷≤ΦΝ–ΓΘ
‘ΧβΫβΈωΘΚΘ®1Θ©’β≈ζ¬÷ΧΞΩμΕ»ΒΡΤΫΨυ÷ΒΈΣ
![]() .
.
Θ®2Θ©![]() ’β≈ζ¬÷ΧΞΩμΕ»ΕΦ‘Ύ
’β≈ζ¬÷ΧΞΩμΕ»ΕΦ‘Ύ![]() ΡΎΒΡΗω ΐΈΣ6Θ§
ΡΎΒΡΗω ΐΈΣ6Θ§
Ι ’β≈ζ¬÷ΧΞΒΎ“Μ¥Έ≥ιΦλΨΆΚœΗώΒΡΗ≈¬ ΈΣ![]() .
.
![]()
![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ1,2Θ§
ΒΡΩ…Ρή»Γ÷ΒΈΣ1,2Θ§ ![]() Θ§
Θ§ ![]() .
.
‘ρ![]() ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
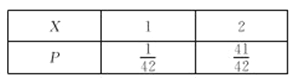
Ι ![]() .
.

ΓΨΧβΡΩΓΩΡ≥–Θ‘ΎΗΏΕΰΡξΦΕ Β––―ΓΩΈΉΏΑύΫΧ―ßΘ§―ß–ΘΈΣ―ß…ζΧαΙ©ΝΥΕύ÷÷ΩΈ≥ΧΘ§Τδ÷– ΐ―ß―ßΩΤΧαΙ©5÷÷≤ΜΆ§≤ψ¥ΈΒΡΩΈ≥ΧΘ§Ζ÷±π≥ΤΈΣ ΐ―ß1ΓΔ ΐ―ß2ΓΔ ΐ―ß3ΓΔ ΐ―ß4ΓΔ ΐ―ß5Θ§ΟΩΗω―ß…ζ÷ΜΡή¥”5÷÷ ΐ―ßΩΈ≥Χ÷–―Γ‘ώ“Μ÷÷―ßœΑΘ§ΗΟ–ΘΗΏΕΰΡξΦΕ1800Οϊ―ß…ζΒΡ ΐ―ß―ΓΩΈ»Υ ΐΆ≥ΦΤ»γ±μΘΚ
ΩΈ≥Χ | ΐ―ß1 | ΐ―ß2 | ΐ―ß3 | ΐ―ß4 | ΐ―ß5 | ΚœΦΤ |
―ΓΩΈ»Υ ΐ | 180 | 540 | 540 | 360 | 180 | 1800 |
ΈΣΝΥΝΥΫβ ΐ―ß≥…Φ®”κ―ß…ζ―ΓΩΈ«ιΩω÷°ΦδΒΡΙΊœΒΘ§”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”’β1800Οϊ―ß…ζ÷–≥ι»Γ10»ΥΫχ––Ζ÷ΈωΘ°
Θ®1Θ©¥”―Γ≥ωΒΡ10Οϊ―ß…ζ÷–ΥφΜζ≥ι»Γ3»ΥΘ§«σ’β3»Υ÷–÷Ν…Ό”–2»Υ―Γ‘ώ ΐ―ß2ΒΡΗ≈¬ ΘΜ
Θ®2Θ©¥”―Γ≥ωΒΡ10Οϊ―ß…ζ÷–ΥφΜζ≥ι»Γ3»ΥΘ§Φ«’β3»Υ÷–―Γ‘ώ ΐ―ß2ΒΡ»Υ ΐΈΣ![]() Θ§―Γ‘ώ ΐ―ß1ΒΡ»Υ ΐΈΣ
Θ§―Γ‘ώ ΐ―ß1ΒΡ»Υ ΐΈΣ![]() Θ§…ηΥφΜζ±δΝΩ
Θ§…ηΥφΜζ±δΝΩ![]() Θ§«σΥφΜζ±δΝΩ
Θ§«σΥφΜζ±δΝΩ![]() ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊ
ΒΡΖ÷≤ΦΝ–ΚΆ ΐ―ßΤΎΆϊ![]() Θ°
Θ°

