题目内容
【题目】已知抛物线的顶点在原点，它的准线过双曲线 
的右焦点，而且与x轴垂直．又抛物线与此双曲线交于点 
，求抛物线和双曲线的方程．
【答案】解：由题意，设抛物线方程为y2=﹣2px（p＞0）
∵抛物线图象过点 
，∴ 
，解之得p=2．
所以抛物线方程为y2=﹣4x，准线方程为x=1．
∵双曲线的右焦点经过抛物线的准线，∴双曲线右焦点坐标为（1，0），c=1
∵双曲线经过点 ，∴ 
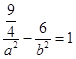
结合c2=a2+b2=1，联解得 
或a2=9，b2=﹣8（舍去）
∴双曲线方程为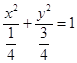 
．
综上所述，抛物线方程为y2=﹣4x，双曲线方程为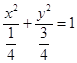
【解析】根据题中的点在抛物线上，列式解出抛物线方程为y2=﹣2x，从而算出双曲线右焦点坐标为（1，0），可得c2=a2+b2=1．再由点 
在双曲线上建立关于a、b的方程，联解得到a、b的值，即可得到双曲线的方程．
练习册系列答案
相关题目
