题目内容
1.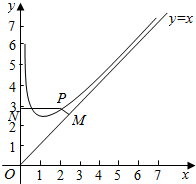 已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.(1)求a的值;
(2)问:PM•PN是否为定值?若是,则求出该定值,若不是,请说明理由;
(3)设O为坐标原点,求四边形OMPN面积的最小值.
分析 (1)可判断a≤0时f (x)递增,没有最小值;从而a>0,结合基本不等式可得$f(x)≥2\sqrt{a}$,从而解得.
(2)设$P({x_0},{x_0}+\frac{{\sqrt{2}}}{x_0})$,从而表示出$PM=\frac{{|{x_0}-({x_0}+\frac{{\sqrt{2}}}{x_0})|}}{{\sqrt{2}}}=\frac{1}{x_0}$,PN=x0,从而得到.
(3)设$P({x_0},{x_0}+\frac{{\sqrt{2}}}{x_0})$,则直线PM:$y-({x_0}+\frac{{\sqrt{2}}}{x_0})=-(x-{x_0})$,联立解得M$({{x_0}+\frac{{\sqrt{2}}}{{2{x_0}}},{x_0}+\frac{{\sqrt{2}}}{{2{x_0}}}})$;从而可得SOMPN=S△OPN+S△OPM=$\frac{1}{2}x_0^2+\frac{1}{2x_0^2}+\sqrt{2}$
≥$2\sqrt{\frac{1}{2}x_0^2•\frac{1}{2x_0^2}}+\sqrt{2}=1+\sqrt{2}$.(当且仅当$\frac{1}{2}x_0^2=\frac{1}{2x_0^2}$,即x0=1时取等号).
解答 解:(1)∵x>0,若a≤0,则f (x)递增,没有最小值,
∴a>0,∴$f(x)≥2\sqrt{a}$,
∴x=$\sqrt{a}$时,$f{(x)_{min}}=2\sqrt{a}=2•\root{4}{2}$;
∴$a=\sqrt{2}$.
(2)设$P({x_0},{x_0}+\frac{{\sqrt{2}}}{x_0})$,
则$PM=\frac{{|{x_0}-({x_0}+\frac{{\sqrt{2}}}{x_0})|}}{{\sqrt{2}}}=\frac{1}{x_0}$,PN=x0,
则PM•PN=1;
(3)设$P({x_0},{x_0}+\frac{{\sqrt{2}}}{x_0})$,则直线PM:$y-({x_0}+\frac{{\sqrt{2}}}{x_0})=-(x-{x_0})$,
由$\left\{\begin{array}{l}y-({x_0}+\frac{{\sqrt{2}}}{x_0})=-(x-{x_0})\\ y=x\end{array}\right.$得,M$({{x_0}+\frac{{\sqrt{2}}}{{2{x_0}}},{x_0}+\frac{{\sqrt{2}}}{{2{x_0}}}})$;
SOMPN=S△OPN+S△OPM=$\frac{1}{2}({x_0}+\frac{{\sqrt{2}}}{x_0})•{x_0}+\frac{1}{2}(\sqrt{2}{x_0}+\frac{1}{x_0})•\frac{1}{x_0}$=$\frac{1}{2}x_0^2+\frac{1}{2x_0^2}+\sqrt{2}$
≥$2\sqrt{\frac{1}{2}x_0^2•\frac{1}{2x_0^2}}+\sqrt{2}=1+\sqrt{2}$.
(当且仅当$\frac{1}{2}x_0^2=\frac{1}{2x_0^2}$,即x0=1时取等号);
故四边形OMPN面积的最小值$1+\sqrt{2}$.
点评 本题考查了函数在几何问题中的应用及基本不等式的应用,同时考查了分类讨论的思想应用,属于中档题.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案 已知某几何体的三视图如图所示,正视图和侧视图是边长为1的正方形,俯视图是腰长为1的等腰直角三角形,则该几何体的体积是( )
已知某几何体的三视图如图所示,正视图和侧视图是边长为1的正方形,俯视图是腰长为1的等腰直角三角形,则该几何体的体积是( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |