题目内容
9.圆x2+y2-8x=0的半径为4.分析 把圆的一般方程化为标准方程,容易得出圆心与半径.
解答 解:∵圆x2+y2-8x=0可化为(x-4)2+y2=16,
∴圆心是(4,0),半径r=4;
故答案为:4.
点评 本题考查了圆的一般方程求圆心与半径的问题,是基础题.

练习册系列答案
相关题目
20.已知x1,x2分别是函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+2bx+c的两个极值点,且x1∈(0,1)x2∈(1,2),则$\frac{b-2}{a-1}$的取值范围为( )
| A. | (1,4) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | ($\frac{1}{4}$,1) |
4.圆x2+y2+2x-4y-4=0的圆心坐标和半径分别是( )
| A. | (-1,2),3 | B. | (-1,2),9 | C. | (1,-2),3 | D. | (1,-2),9 |
14.在三角形ABC中,三个内角所对的边为a,b,c,如果A:B:C=1:2:3,那么a:b:c=( )
| A. | 1:2:3 | B. | 1:$\sqrt{3}$:2 | C. | 1:4:9 | D. | 1:$\sqrt{2}$:$\sqrt{3}$ |
19.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y≤2}\\{x-y≥-1}\\{x+y≥1}\end{array}\right.$,则z=x2+y2的范围是( )
| A. | [1,5] | B. | [1,25] | C. | [$\frac{1}{2}$,25] | D. | [$\frac{\sqrt{2}}{2}$,5] |
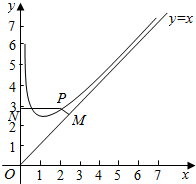 已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.