题目内容
11．定义在R上的可导函数f（x），已知y=f′（x）的图象如图所示，则y=f（x）的增区间是R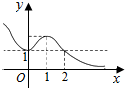
分析 通过图象得到f′（x）＞0在R上恒成立，从而求出函数f（x）的单调区间．
解答 解：由图象得：f′（x）＞0在R上恒成立，
∴函数y=f（x）在R上递增，
故答案为：R．
点评 本题考查了函数的单调性，考查导数的应用，是一道基础题．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
1．因为对数函数y=logax（a＞0，且a≠1）是增函数，而y=log${\;}_{\frac{1}{2}}$x是对数函数，所以y=log${\;}_{\frac{1}{2}}$x是增函数，上面的推理错误的是（ ）
| A． | 大前提 | B． | 小前提 | C． | 推理形式 | D． | 以上都是 |
6．已知f（x）=$\left\{\begin{array}{l}{3|lo{g}_{3}x|，0＜x≤3}\\{（x-4）（x-6），x＞3}\end{array}\right.$，若f（a）=f（b）=f（c）=f（d），且a＜b＜c＜d，则abcd的取值范围是（ ）
| A． | （23，24） | B． | （24，27） | C． | （21，24） | D． | （24，25） |
3．若变量x，y满足约束条件：$\left\{{\begin{array}{l}{0≤x≤7}\\{2≤y≤8}\\{3x-y≥1}\end{array}}\right.$，则变量z=x-y的取值情况是（ ）
| A． | 既没有最大值也没有最小值 | B． | 有最大值5，没有最小值 | ||
| C． | 有最小值-1，没有最大值 | D． | 有最小值-5，也有最大值5 |
20．已知x1，x2分别是函数f（x）=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+2bx+c的两个极值点，且x1∈（0，1）x2∈（1，2），则$\frac{b-2}{a-1}$的取值范围为（ ）
| A． | （1，4） | B． | （$\frac{1}{2}$，1） | C． | （$\frac{1}{4}$，$\frac{1}{2}$） | D． | （$\frac{1}{4}$，1） |
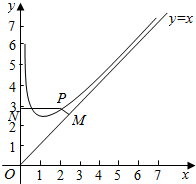已知函数f（x）=x+$\frac{a}{x}$ （x＞0）的最小最小值为$2•\root{4}{2}$，设点P是函数图象上的任意一点，过点P分别作直线y=x和y轴的垂线，垂足分别为M、N．