题目内容
16.在△ABC中,角A、B、C所对的边为a、b、c,若b=acosC且△ABC的最大边长为12,最小角的正弦值为$\frac{1}{3}$.(1)判断△ABC的形状;
(2)求△ABC的面积.
分析 (1)依题意,利用正弦定理可得sinAcosC=sinB,再利用诱导公式与两角和的正弦公式得到cosAsinC=0,从而可判断△ABC的形状.
(2)由题意可求最小角所对的边长为:12×$\frac{1}{3}$=4,另一直角边为:$\sqrt{1{2}^{2}-{4}^{2}}$=8$\sqrt{2}$,从而可求三角形面积.
解答 解:(1)在△ABC中,∵acosC=b,
∴sinAcosC=sinB=sin[π-(A+C)]=sin(A+C)=sinAcosC+cosAsinC,
∴cosAsinC=0,sinC>0,
∴cosA=0,A=90°,
∴△ABC的形状是直角三角形,
(2)∵A=90°,且△ABC的最大边长为12,最小角的正弦值为$\frac{1}{3}$.
∴最小角所对的边长为:12×$\frac{1}{3}$=4,另一直角边为:$\sqrt{1{2}^{2}-{4}^{2}}$=8$\sqrt{2}$,
∴S△ABC=$\frac{1}{2}$×$4×8\sqrt{2}$=16$\sqrt{2}$.
点评 本题考查三角形的形状的判断及三角形面积的求法,着重考查正弦定理,勾股定理与两角和的正弦公式的应用,属于中档题.

练习册系列答案
相关题目
6.已知f(x)=$\left\{\begin{array}{l}{3|lo{g}_{3}x|,0<x≤3}\\{(x-4)(x-6),x>3}\end{array}\right.$,若f(a)=f(b)=f(c)=f(d),且a<b<c<d,则abcd的取值范围是( )
| A. | (23,24) | B. | (24,27) | C. | (21,24) | D. | (24,25) |
7.盒中装有10个乒乓球,其中6个新球,4个旧球,不放回地依次取出2个球使用,在第一次取出新球的条件下,第二次也取到新球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{5}$ |
4.圆x2+y2+2x-4y-4=0的圆心坐标和半径分别是( )
| A. | (-1,2),3 | B. | (-1,2),9 | C. | (1,-2),3 | D. | (1,-2),9 |
8.现有l位教师,2位男同学,3位女同学共6人站成一排,则2位男同学站首尾两端,且3位女同学中有且仅有两位相邻的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{20}$ | C. | $\frac{1}{30}$ | D. | $\frac{1}{60}$ |
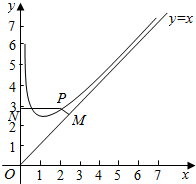 已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.