题目内容
11.已知a∈R,直线l:(a-1)x+ay+3=0,则直线l经过的定点的坐标为(3,-3).分析 把直线的方程化为m(ax+by+c)+(a′x+b′y+c′)=0的形式,再令m的系数等于零,即可求得定点的坐标.
解答 解:直线l:(a-1)x+ay+3=0,即 a(x+y)+(-x+3)=0,
令x+y=0,可得-x+3=0,求得x=3,y=-3,故直线l经过的定点的坐标为(3,-3),
故答案为:(3,-3).
点评 本题主要考查直线过定点问题,利用了m(ax+by+c)+(a′x+b′y+c′)=0 经过直线ax+by+c=0和直线a′x+b′y+c′=0的交点,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y≤2}\\{x-y≥-1}\\{x+y≥1}\end{array}\right.$,则z=x2+y2的范围是( )
| A. | [1,5] | B. | [1,25] | C. | [$\frac{1}{2}$,25] | D. | [$\frac{\sqrt{2}}{2}$,5] |
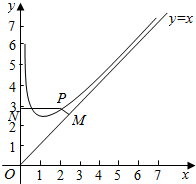 已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.