题目内容
6.已知等式:sin25°+cos235°+sin5°cos35°=$\frac{3}{4}$; sin215°+cos245°+sin15°cos45°=$\frac{3}{4}$;sin230°+cos260°+sin30°cos60°=$\frac{3}{4}$;由此可归纳出对任意角度θ都成立的一个等式,并予以证明.
分析 根据所给的等式归纳:等式左边余弦均为正弦度数加30°,右边是常数,按照此规律写出一般性的结论,利用两角和的余弦公式等进行证明等式成立.
解答 解:根据各式的共同特点可得:等式左边余弦均为正弦度数加30°,右边是常数$\frac{3}{4}$,
则具有一般规律的等式:sin2θ+cos2(θ+30°)+sinθcos(θ+30°)=$\frac{3}{4}$,
证明:等式的左边=sin2θ+cos(θ+30°)[cos(θ+30°)+sinθ]
=sin2θ+($\frac{\sqrt{3}}{2}$cosθ-$\frac{1}{2}$sinθ)($\frac{\sqrt{3}}{2}cosθ-\frac{1}{2}sinθ$+sinθ)
=sin2θ+($\frac{3}{4}co{s}^{2}θ-\frac{1}{4}si{n}^{2}θ$)
=$\frac{3}{4}co{s}^{2}θ+\frac{3}{4}si{n}^{2}θ$=$\frac{3}{4}$=右边,
∴等式成立.
点评 本题考查了归纳推理,两角和的余弦公式等,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在三角形ABC中,三个内角所对的边为a,b,c,如果A:B:C=1:2:3,那么a:b:c=( )
| A. | 1:2:3 | B. | 1:$\sqrt{3}$:2 | C. | 1:4:9 | D. | 1:$\sqrt{2}$:$\sqrt{3}$ |
11.圆心为(2,-1)且经过点(-1,3)的圆的标准方程是( )
| A. | (x-2)2+(y+1)2=25 | B. | (x+2)2+(y-1)2=25 | C. | (x-2)2+(y+1)2=5 | D. | (x+2)2+(y-1)2=5 |
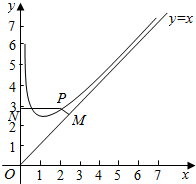 已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
已知函数f(x)=x+$\frac{a}{x}$ (x>0)的最小最小值为$2•\root{4}{2}$,设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.